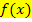Die Integralfunktion und der HDI
Die untere Grenze a wird deshalb ermittelt, indem man die Nullstelle(n) von 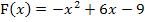 berechnet. Kommen mehrere Nullstellen heraus, kann man sich eine aussuchen. Dann gibt es also mehrere Möglichkeiten für die untere Grenze a. Du musst auf jeden Fall die Nullstelle(n) von F(x) berechnen, d.h. F(x) gleich Null setzen und nach x auflösen. Es wird dann ganz sicher mindestens eine Lösung geben, denn laut Angabe ist F(x) ja eine Integralfunktion und Integralfunktionen haben immer mindestens eine Nullstelle. (Hätte F(x) keine Nullstelle, gäbe es schließlich keinen Wert für die untere Grenze a und F(x) ließe sich nicht in der Form
berechnet. Kommen mehrere Nullstellen heraus, kann man sich eine aussuchen. Dann gibt es also mehrere Möglichkeiten für die untere Grenze a. Du musst auf jeden Fall die Nullstelle(n) von F(x) berechnen, d.h. F(x) gleich Null setzen und nach x auflösen. Es wird dann ganz sicher mindestens eine Lösung geben, denn laut Angabe ist F(x) ja eine Integralfunktion und Integralfunktionen haben immer mindestens eine Nullstelle. (Hätte F(x) keine Nullstelle, gäbe es schließlich keinen Wert für die untere Grenze a und F(x) ließe sich nicht in der Form 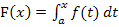 schreiben. Dann wäre F(x) eben keine Integralfunktion.)
schreiben. Dann wäre F(x) eben keine Integralfunktion.)
Die Integrandenfunktion  findest du, indem du F(x) ableitest. Es gilt schließlich der HDI:
findest du, indem du F(x) ableitest. Es gilt schließlich der HDI: 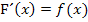
Nun kannst du die Aufgabe bestimmt auch alleine lösen. Los geht´s!
Zu deiner Kontrolle im Folgenden der komplette Rechenweg.
Nullstelle von F berechnen, um die untere Grenze a zu ermitteln:
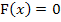
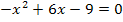
Diese Gleichung kann nun entweder mit der Mitternachtsformelgelöst werden, oder indem man ein Minus ausklammert und die zweite binomische Formel 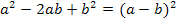 anwendet. Dass man hier nach dem Ausklammern von -1, d.h. des Minuszeichens, eine binomische Formel anwenden kann, muss man natürlich erst einmal erkennen. Das ist nicht so leicht. Jetzt denkst du dir wahrscheinlich:„Das hätte ich alleine niemals erkannt!“ Ist ja nicht schlimm, du kannst ja genauso gut die Mitternachtsformel verwenden.
anwendet. Dass man hier nach dem Ausklammern von -1, d.h. des Minuszeichens, eine binomische Formel anwenden kann, muss man natürlich erst einmal erkennen. Das ist nicht so leicht. Jetzt denkst du dir wahrscheinlich:„Das hätte ich alleine niemals erkannt!“ Ist ja nicht schlimm, du kannst ja genauso gut die Mitternachtsformel verwenden.
1. Methode:Mit der Mitternachtsformel
Zur Erinnerung:Gleichungen der Form 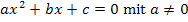 können mit der folgenden Formel gelöst werden:
können mit der folgenden Formel gelöst werden:

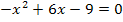
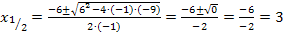
2. Methode:Minus ausklammern und danach binomische Formel anwenden
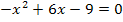
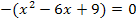
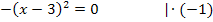
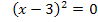
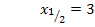
Die Funktion 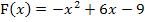 hat also eine (doppelte) Nullstelle bei
hat also eine (doppelte) Nullstelle bei 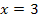 . Die untere Grenze a liegt somit bei
. Die untere Grenze a liegt somit bei 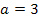 .
.
Integrandenfunktion 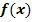 ermitteln, d.h. F(x) ableiten:
ermitteln, d.h. F(x) ableiten:
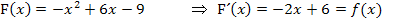
Die Integrandenfunktion ist somit 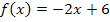 .
.
Man kann die Integralfunktion 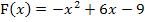 daher auch in der folgenden Form schreiben:
daher auch in der folgenden Form schreiben: 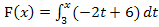
An diesem Aufgabenbeispiel konntest du sehen, wie man von der integralfreien Darstellung einer Integralfunktion auf die Integraldarstellung dieser Funktion kommt.
| Kurze Zusammenfassung dessen, was du an diesem Aufgabenbeispiel lernen solltest
Wie man von der integralfreien Form einer Integralfunktion F(x) zu ihrer Integraldarstellung Die Nullstelle von F(x) entspricht der unteren Grenze a. Die Ableitung F´(x) entspricht laut HDI der Integrandenfunktion In der Integraldarstellung muss bei f allerdings t an Stelle von x geschrieben werden. |
Nun wollen wir uns mit Aufgaben beschäftigen, die ausschließlich mit Hilfe des HDI gelöst werden können, d.h. ohne Verwendung der integralfreien Darstellung der Integralfunktion.

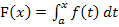 kommt:
kommt: