Die Integralfunktion und der HDI
Daraus folgt:Jede Integralfunktion F einer stetigen Funktion f ist auch Stammfunktion zu f.
Aber Vorsicht:Nicht jede Stammfunktion ist auch Integralfunktion!
Die Integralfunktion 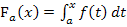 hat nämlich mindestens eine Nullstelle, eine Stammfunktion muss dagegen keine Nullstellen haben. Eine Integralfunktion hat immer bei
hat nämlich mindestens eine Nullstelle, eine Stammfunktion muss dagegen keine Nullstellen haben. Eine Integralfunktion hat immer bei 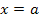 , d.h. bei ihrer unteren Grenze, eine Nullstelle. Das liegt daran, dass das Integral
, d.h. bei ihrer unteren Grenze, eine Nullstelle. Das liegt daran, dass das Integral 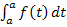 auf jeden Fall gleich Null ist;dabei existiert schließlich keine Fläche. Ist die obere mit der unteren Grenze identisch, muss das Integral zwangsläufig gleich Null ergeben. Eine Integralfunktion hat daher bei ihrer unteren Grenze immer eine Nullstelle.
auf jeden Fall gleich Null ist;dabei existiert schließlich keine Fläche. Ist die obere mit der unteren Grenze identisch, muss das Integral zwangsläufig gleich Null ergeben. Eine Integralfunktion hat daher bei ihrer unteren Grenze immer eine Nullstelle.
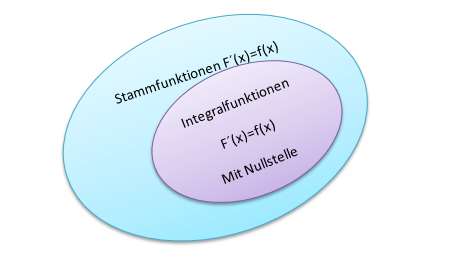
Wie du an der Graphik erkennen kannst, sind die Integralfunktionen eine Teilmenge der Stammfunktionen. Die Bezeichnung „Integralfunktion“ ist also genauer als „Stammfunktion“.
Nun einige typische Fragestellungen rund um das Thema Integralfunktion.
Wie beweist man, dass eine gegebene Funktion F(x) eine Integralfunktion zu 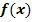 ist? ist?
1. Nachweisen, dass gilt: D.h. Man leitet F(x) ab und formt so lange um, bis man auf die Gleichung von 2. Nachweisen, dass F(x) mindestens eine Nullstelle hat. Die Gleichung F(x) = 0 muss also mindestens eine Lösung besitzen. In anderen Worten:Man setzt F(x) gleich Null und löst nach x auf. Dabei muss mindestens eine Lösung herauskommen. Damit ist gezeigt, dass F(x) wirklich eine Integralfunktion und nicht nur Stammfunktion zu
|
2. Bsp.:
Untersuche, ob die Funktion 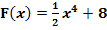 eine Integralfunktion ist!
eine Integralfunktion ist!
Lösung:
Wenn die Funktion F(x) keine Nullstellen hat, kann sie auch keine Integralfunktion sein. Wir überprüfen daher, ob F(x) Nullstellen besitzt. Wir setzen F(x) gleich Null und versuchen nach x aufzulösen.
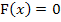
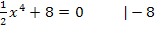
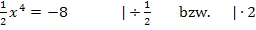
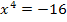
Jetzt müsste man eigentlich die vierte Wurzel ziehen, um nach x aufzulösen. Aus einer negativen Zahl lässt sich jedoch die vierte Wurzel nicht ziehen. 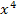 ist eine gerade Potenz und gerade Potenzen können nicht negativ sein. Deshalb hat die Gleichung
ist eine gerade Potenz und gerade Potenzen können nicht negativ sein. Deshalb hat die Gleichung 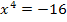 keine Lösung.
keine Lösung.
Daraus folgt:F(x) hat keine Nullstellen und ist deshalb sicher keine Integralfunktion.
3. Bsp.:
Die Funktion 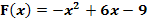 ist eine Integralfunktion und lässt sich daher auch in der Form
ist eine Integralfunktion und lässt sich daher auch in der Form 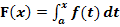 schreiben. Ermittle die untere Grenze a und die zugehörige Integrandenfunktion
schreiben. Ermittle die untere Grenze a und die zugehörige Integrandenfunktion 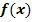 !
!
Lösung:
Wir wissen, dass eine Integralfunktion F(x) immer bei x = a eine Nullstelle hat.

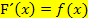
 kommt. Dadurch ist schon ´mal gezeigt, dass F(x) eine Stammfunktion zu
kommt. Dadurch ist schon ´mal gezeigt, dass F(x) eine Stammfunktion zu 