Die Integralfunktion und der HDI
So kamen wir als Zwischenergebnis zur Integralfunktion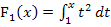 
bzw. in integralfreier Form 
.
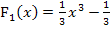Nun leite doch ´mal die Integralfunktion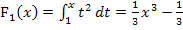 
ab! Was stellst du dabei fest?
Zur Erinnerung:Eine Funktion der Form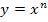 
wird mit der Regel 
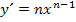abgeleitet, d.h. den ursprünglichen Exponenten nach vorne ziehen und außerdem beim Exponenten 1 abziehen. Additive Konstanten, also Zahlen ohne x, die addiert oder subtrahiert werden, fallen beim Ableiten weg.
Die Integralfunktion 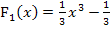ergibt somit abgeleitet:
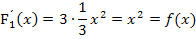
Es kommt also beim Ableiten von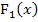 
wieder genau 
heraus. Das ist natürlich kein Zufall. Für jede Integralfunktion gilt der Hauptsatz der Differenzial- und Integralrechnung, kurz HDI. Damit ist Folgendes gemeint:
 |
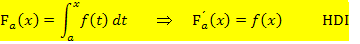Das leuchtet dir sicherlich ein. Denn, wenn du eine Funktion zuerst integrierst und dann wieder ableitest, bekommst du wieder selbst heraus. Im Prinzip besagt der HDI nur, dass sich Integrieren und Ableiten wieder gegenseitig aufheben. Der HDI gilt übrigens nur für stetige Funktionen , also Funktionen ohne Sprungstellen. (Siehe auch:Stetigkeit) Auf den Beweis des HDI wird hier verzichtet;er ist kompliziert und du brauchst ihn sowieso nicht.
Den Zusammenhang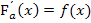 
kann man oft praktisch nutzen, wenn man die Ableitung einer Integralfunktion 
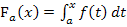benötigt:Einfach die Funktion hinter dem Integralzeichen nehmen und statt t einfach x schreiben;schon hat man die Ableitung 
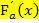der Integralfunktion! Also nicht erst integrieren und dann wieder ableiten! Du kannst somit auch die Ableitung einer Integralfunktion angeben, wenn du das Integral gar nicht ausrechnen kannst! Die Ableitung 
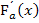der Integralfunktion 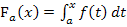wird nicht durch die untere Grenze a beeinflusst. Die untere Grenze a ist dabei völlig egal.
Beispiel:
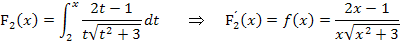
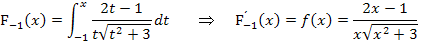
Die beiden Integralfunktionen unterscheiden sich nur in ihrer unteren Grenze, daher haben sie auch beide die gleiche Ableitung. Bitte versuche erst gar nicht diese beiden Integralfunktionen integralfrei zu schreiben, d.h. sie auszurechnen. Das klappt nicht! Diese Integrale sind viel zu kompliziert, als dass du sie lösen könntest. Sie wurden absichtlich so gewählt, damit du daran erkennst, dass der Zusammenhang 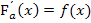bei Integralfunktionen sehr wichtig und hilfreich ist.
Unterschied zwischen Integralfunktion und Stammfunktion
Den Zusammenhang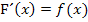 
hast du schon einmal gelernt. Hoffentlich kannst du dich noch daran erinnern.
Für jede Stammfunktion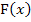 
zu einer stetigen Funktion gilt nämlich: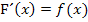
Das ist schließlich die Definition einer Stammfunktion.
