Die Integralfunktion und der HDI
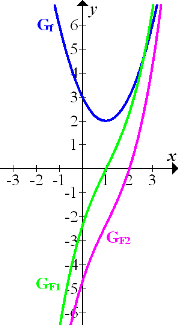
Abb.:Graph 
der Integrandenfunktion 
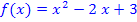sowie die Graphen 
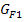und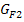 
der zugehörigen Integralfunktionen 
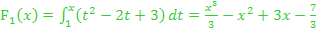und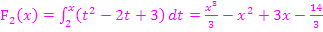 
Zu 1c.)
Hier noch einmal die Angabe: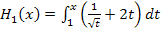 
Bevor wir hier integrieren können, müssen wir die Integrandenfunktion (d.h. den Ausdruck direkt hinter dem Integralzeichen) geeignet umformen. Wir brauchen dazu die Potenzgesetze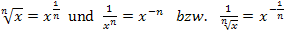 
. Versuche es gleich ´mal alleine!
Zu deiner Kontrolle folgt nun der ausführliche Rechenweg:
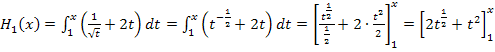
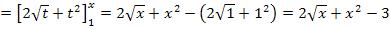
Fertig!
Die Integralfunktion 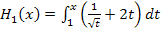hat für 
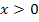die integralfreie Darstellung:
.
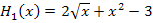Nun hast du hoffentlich verstanden, wie man von der Integraldarstellung einer Integralfunktion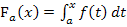 
zu ihrer integralfreien Darstellung kommt. Die integralfreie Darstellung kannst du allerdings nur dann ermitteln, wenn du überhaupt eine Stammfunktion finden kannst. Eben dies geht nicht immer. (An sich schon, bloßmusst du das für das Abitur nicht immer können.) Doch wirst du etwas weiter unten noch sehen, dass es oftmals gar nicht nötig ist, die integralfreie Darstellung zu berechnen.
Wozu aber überhaupt eine Funktion der Form 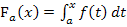verwenden?
Wenn man beispielsweise die bestimmten Integrale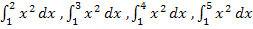 
und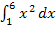 
berechnen muss, so kann man auch folgendermaßen vorgehen:Man berechnet zuerst 
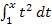und setzt nachher für x die Werte 2, 3, 4, 5 und 6 ein. Das geht viel schneller, als die Integrale jeweils einzeln zu berechnen.
Das klappt natürlich nur, weil sich alle erwähnten Integrale auf die gleiche Funktion 
, hier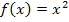 
, beziehen und alle Integrale auch die selbe untere Grenze, hier a = 1, besitzen. Man kann also die Integralfunktion 
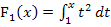verwenden, diese in einem ersten Schritt ausrechnen und damit nachher die Werte 
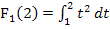sowie 
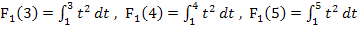und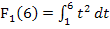 
ermitteln. Jetzt machen wir das doch gleich einmal.
1. Integralfunktion integralfrei schreiben, d.h. Stammfunktion ermitteln und dann die Grenzen x und 1 einsetzen, zuerst die obere Grenze x minus die untere 1.
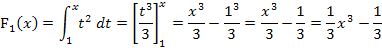
Das vorliegende Ergebnis ist die oben schon erwähnte integralfreie Form der Integralfunktion. Die integralfreie Form ist ja die ausgerechnete Form der Integralfunktion. Sie enthält, wie der Name schon verrät, kein Integral mehr.
2. Für x die entsprechenden Werte in die integralfreie Form einsetzen, dadurch erhält man die Ergebnisse der gesuchten bestimmten Integrale.
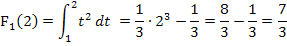
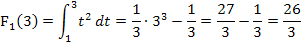
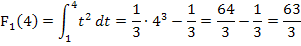
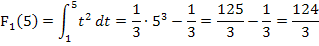
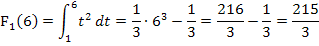
Es hätte viel länger gedauert, die Integrale einzeln zu berechnen. Daher war es wesentlich praktischer vorweg als obere Grenze x zu wählen und erst später die jeweiligen konkreten oberen Grenzen einzusetzen.
