Die Integralfunktion und der HDI
Soll beispielsweise die y-Koordinate des Kurvenpunktes P(5|?) von F ermittelt werden, muss F(5) abgeschätzt werden. (x = 5 ist irgendein willkürlich gewähltes Beispiel.) Aus 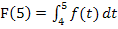 erhältst du die y-Koordinate von P. Du musst daher die Fläche zwischen
erhältst du die y-Koordinate von P. Du musst daher die Fläche zwischen  und der x-Achse von
und der x-Achse von 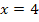 bis
bis  abschätzen. Weil 5 größer ist als 4, integriert man dabei in die „richtige“ Richtung. Die Fläche liegt unterhalb der x-Achse;sie zählt negativ. Die gesuchte y-Koordinate von P ist daher negativ.
abschätzen. Weil 5 größer ist als 4, integriert man dabei in die „richtige“ Richtung. Die Fläche liegt unterhalb der x-Achse;sie zählt negativ. Die gesuchte y-Koordinate von P ist daher negativ.
Soll dagegen beispielsweise die y-Koordinate des Kurvenpunktes Q(1|?) von F ermittelt werden, muss F(1) abgeschätzt werden. (x = 1 ist irgendein anderes willkürlich gewähltes Beispiel.) Aus  erhältst du die y-Koordinate von Q. Du musst daher die Fläche zwischen
erhältst du die y-Koordinate von Q. Du musst daher die Fläche zwischen  und der x-Achse von
und der x-Achse von 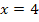 bis
bis 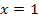 abschätzen. Weil 1 kleiner ist als 4, integriert man dabei in die „falsche“ Richtung. Die Fläche liegt oberhalb der x-Achse;sie zählt wegen der „falschen“ Integrationsrichtung negativ. Die gesuchte y-Koordinate von Q ist daher negativ.
abschätzen. Weil 1 kleiner ist als 4, integriert man dabei in die „falsche“ Richtung. Die Fläche liegt oberhalb der x-Achse;sie zählt wegen der „falschen“ Integrationsrichtung negativ. Die gesuchte y-Koordinate von Q ist daher negativ.
Nun zurück zum Krümmungsverhalten und den Wendepunkten von 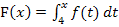 .
.
Hier noch einmal der Graph von f.
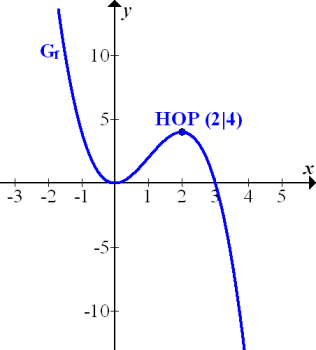
Abb.:Graph 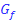
Aus der Abbildung ist zu entnehmen:Die Funktion f hat im Ursprung einen Tiefpunkt und im Punkt (2|4) einen Hochpunkt. (Die Koordinaten des Hochpunktes von f sind sogar extra in der Aufgabenstellung angegeben.) Für 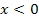 fällt
fällt  streng monoton, für
streng monoton, für 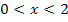 steigt
steigt  streng monoton und für
streng monoton und für  ist er wieder streng monoton fallend. Was bedeutet das für die Integralfunktion F?
ist er wieder streng monoton fallend. Was bedeutet das für die Integralfunktion F?
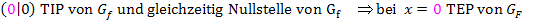
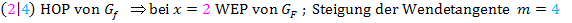
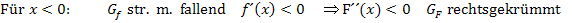
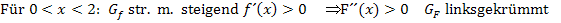
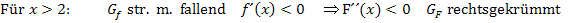
Wir fassen noch einmal alles in einer Krümmungstabelle von F zusammen.
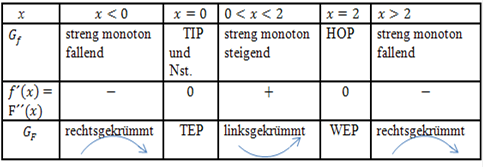
Es ist noch die y-Koordinate des Wendepunktes WEP(2|?) von F anzugeben. Wir müssen also 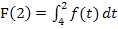 ermitteln. Wäre in der Aufgabe nur der Graph von f gegeben, müssten wir jetzt die Flächenbilanz von x = 4 bis x = 2 abschätzen. Doch in dieser Aufgabe ist ja noch etwas anderes gegeben. Laut Angabe gilt:
ermitteln. Wäre in der Aufgabe nur der Graph von f gegeben, müssten wir jetzt die Flächenbilanz von x = 4 bis x = 2 abschätzen. Doch in dieser Aufgabe ist ja noch etwas anderes gegeben. Laut Angabe gilt: 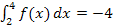
Wenn man die Grenzen vertauscht, erhalten wir das benötigte Integral 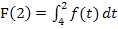 . Durch das Vertauschen der Grenzen dreht sich allerdings das Vorzeichen des Integrals um. Damit lässt sich F(2) nun leicht angeben.
. Durch das Vertauschen der Grenzen dreht sich allerdings das Vorzeichen des Integrals um. Damit lässt sich F(2) nun leicht angeben.

Der Wendepunkt von F lautet somit:WEP(2|4)
Hinweis:Dass in diesem Fall die y-Koordinate des Wendepunktes von F mit der y-Koordinate des Extremums von f übereinstimmt, ist reiner Zufall. In anderen Aufgaben wird das eher selten der Fall sein.

