Die Integralfunktion und der HDI
In den Bereichen, wo der Graph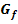 
streng monoton fällt, ist die erste Ableitung 
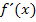negativ und somit auch die zweite Ableitung 
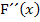negativ, d.h. der Graph der Integralfunktion 
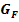ist dort rechtsgekrümmt.
Wo der Graph 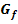ein Extremum hat, gilt 
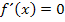mit Vorzeichenwechsel von 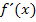und somit ist dort auch die zweite Ableitung der Integralfunktion 
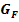mit Vorzeichenwechsel von F´´(x), was bedeutet, dass der Graph an dieser Stelle einen Wendepunkt hat.
Die x-Koordinate des Wendepunktes von F ergibt sich also aus der x-Koordinate des Extremums von f. Die y-Koordinate des Wendepunktes/Terrassenpunktes von F entspricht natürlich nicht automatisch der y-Koordinate des Extremums von f, sondern der Flächenbilanz ausgehend von der unteren Grenze der Integralfunktion bis zum jeweiligen x-Wert.
Die Steigung der Wendetangente von F ergibt sich aus der y-Koordinate des Extremums von f. Das folgt aus dem HDI, also dem Zusammenhang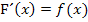 
. (Dies bedeutet ja nichts anderes als, dass die Steigung von F an einer bestimmten Stelle x dem Funktionswert von f an der Stelle x entspricht.)
Wenn der Graph von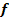 
einen Extrempunkt hat, der gleichzeitig Nullstelle ist, d.h. wenn 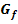die x-Achse berührt, also nicht schneidet, besitzt der Graph von F an dieser Stelle einen Terrassenpunkt, d.h. einen Wendepunkt mit waagrechter Tangente. Das liegt daran, dass bei einer Nullstelle von f die y-Koordinate 
gleich Null ist und wegen 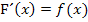auch die Steigung von F, d.h. 
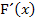gleich Null ist. Die Wendetangente von F verläuft daher waagrecht. Ein Wendepunkt mit waagrechter Tangente wird bekanntlich als Terrassenpunkt, kurz TEP, bezeichnet.
Ist bloßder Graph von f gegeben, kann die y-Koordinate eines Punktes von F nur grob geschätzt werden. Du versuchst dann die Flächenstücke oberhalb und unterhalb der x-Achse zu schätzen, indem du abzählst, wie viele Kästchen ungefähr hinein passen. Bei einem Maßstab von 1 cm auf beiden Achsen ergeben 4 Kästchen genau 1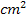 
.
Vorsicht bei den Vorzeichen:Immer bei der angegebenen unteren Grenze der Integralfunktion F mit der Integration beginnen. Nur wenn du dabei von links nach rechts also in die „richtige“ Richtung, integrierst, zählen Flächenstücke oberhalb der x-Achse positiv und die unterhalb der x-Achse negativ.
Integrierst du in die andere Richtung – du musst ja immer von der vorgegebenen unteren Grenze von F ausgehen – drehen sich die Vorzeichen entsprechend um!
In unserem Beispiel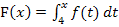 
ist die untere Grenze 4. Willst du die y-Koordinate eines Kurvenpunktes von F abschätzen, musst du in Gedanken immer bei x = 4 starten.
