Die Integralfunktion und der HDI
Die Integrale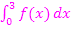 
und 
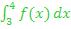sind vom Betrag her gleich groß. Betrachte dazu auch die folgende Abbildung! Die rosa schraffierte Fläche ist tatsächlich genauso großwie die grün schraffierte, auch wenn man das nur an Hand der Zeichnung nicht sofort glauben würde.
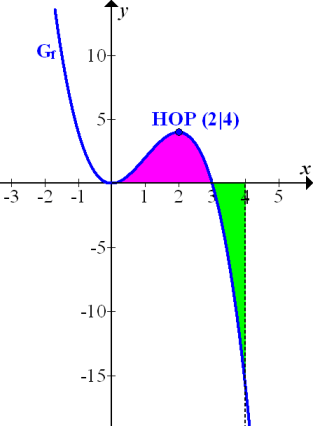
Abb.:Graph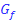 
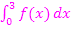mit und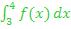
Für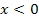 
hat F keine weiteren Nullstellen, da der Graph von 
in diesem Bereich komplett oberhalb der x-Achse verläuft. Es können sich daher keine Flächenstücke oberhalb der x-Achse mit welchen, die unterhalb liegen, ausgleichen bzw. wegheben. Die Flächenbilanz kann somit für negative x nicht gleich Null werden.
F hat genau zwei Nullstellen: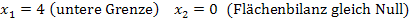 
Extrema und Monotonie von F:
Laut HDI gilt: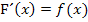 
Die Steigung von F entspricht also den y-Werten von f.
Um die Extrema von F zu berechnen, muss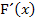 
gleich Null gesetzt werden, was dem Gleichnullsetzen von entspricht. Wie du von der Kurvendiskussion einer Funktion weißt, ergeben sich aus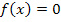 
die Nullstellen von f. Daraus folgt:F kann nur an denjenigen Stellen Extrema haben, wo f Nullstellen besitzt. (Diesen Zusammenhang haben wir auch bei der Stammfunktion F schon kennengelernt. Siehe auch:Die Stammfunktion F(x) und einfache Integrationsregeln) Ein Extremum von F liegt aber nur dann vor, wenn sich das Vorzeichen von 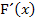bzw. ändert.
Zur Erinnerung:Es muss sich das Steigungsverhalten einer Funktion ändern, damit wirklich ein Extremum vorliegt. Ist zwar die Tangente waagrecht, also die erste Ableitung gleich Null, aber es liegt kein Vorzeichenwechsel der Ableitung vor, so handelt es sich um einen Terrassenpunkt und nicht um ein Extremum der Funktion.
Zusammenhang des Verlaufs von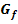 
mit dem Steigungsverhalten von 
:
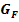In den Bereichen, wo der Graph 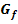oberhalb der x-Achse verläuft, ist die y-Koordinate von 
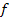positiv und somit auch die erste Ableitung 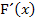der Integralfunktion F positiv, d.h. der Graph der Integralfunktion 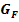steigt dort streng monoton.
In den Bereichen, wo der Graph 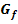unterhalb der x-Achse verläuft, ist die y-Koordinate von 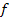negativ und somit auch die erste Ableitung 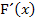der Integralfunktion F negativ, d.h. der Graph der Integralfunktion 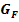fällt dort streng monoton.
Wo der Graph 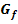eine Nullstelle hat, gilt für die y-Koordinate von 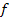an dieser Stelle 
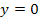bzw. 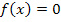und somit ist dort auch die erste Ableitung der Integralfunktion 
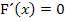, was bedeutet, dass der Graph 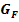an dieser Stelle einen Punkt mit waagrechter Tangente hat.
Nur wo der Graph von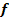 
die x-Achse schneidet, d.h. wo 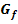eine einfache Nullstelle hat, besitzt der Graph von F ein Extremum, d.
