Die Integralfunktion und der HDI
Nun muss die Frage beantwortet werden, ob F noch weitere Nullstellen besitzt. Dazu betrachten wir den Graph 
der Integrandenfunktion 
und überlegen uns, ob die Flächenbilanz von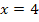 
ausgehend Null ergeben kann. Damit die Flächenbilanz gleich Null wird, muss der Flächenanteil unterhalb der x-Achse genauso großsein wie der oberhalb der x-Achse.
Wenn man von 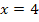auf der x-Achse nach rechts geht, verläuft der Graph ausschließlich unterhalb der x-Achse. Die Fläche zwischen und der x-Achse liegt für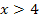 
komplett unterhalb der x-Achse. Für 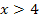ist das Integral 
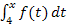daher immer negativ;es kann nicht gleich Null werden;es existieren im Bereich 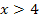keine Nullstellen.
Nun gehen wir in Gedanken von 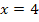auf der x-Achse nach links. Dann gilt 
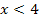. Bei 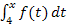stellt x die obere Grenze dar. Für 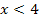ist die obere Grenze kleiner als die untere;wir integrieren praktisch von rechts nach links, also in die „falsche“ Richtung. Daher werden die Flächenstücke oberhalb der x-Achse negativ und die unterhalb positiv gezählt. Die Flächenbilanz ist trotzdem gleich Null, wenn die Flächenstücke oberhalb und unterhalb gleich großsind. An der Abbildung ist zu erkennen, dass der Graph der Integrandenfunktion die x-Achse bei 
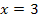schneidet und bei 
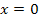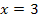berührt. Die Fläche zwischen und der x-Achse von bis 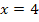liegt unterhalb der x-Achse. Da wir aber in die „falsche“ Richtung, nämlich von 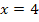bis 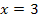integrieren, ist das Integral 
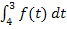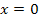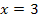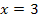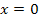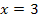positiv. Die Fläche zwischen und der x-Achse von bis liegt oberhalb der x-Achse. Wir integrieren aber in die falsche Richtung, deshalb zählt dieses Flächenstück negativ. Die Frage ist nun, wie weit man von (bis höchstens ) nach links gehen muss, damit diese Fläche zwischen und der x-Achse genauso großist, wie die Fläche zwischen und der x-Achse von bis 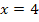. Diese Frage kann man nur mit Hilfe der angegebenen Integrale 
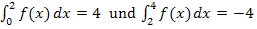exakt beantworten. Die obere Grenze des ersten Integrals fällt mit der unteren des zweiten Integrals zusammen;wir können die beiden Integrale zusammenfassen:
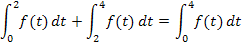
Wir kennen die Werte der beiden Integrale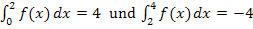 
. Damit ergibt sich:
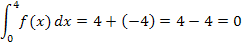
Bei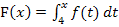 
ist die untere Grenze 4. Wir müssen also noch die Grenzen bei 
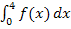vertauschen. Wenn man die Grenzen eines Integrals vertauscht, dreht sich das Vorzeichen des Ergebnisses um. Da hier das Ergebnis jedoch 0 ist, spielt das Vorzeichen keine Rolle. Es gilt: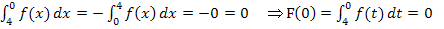 
Die Integralfunktion 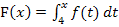hat somit bei 
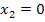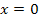eine weitere Nullstelle. Daraus folgt:Die Fläche zwischen und der x-Achse von bis 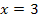liegt oberhalb der x-Achse und ist genauso großwie die Fläche von 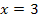bis .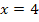
