Die Integralfunktion und der HDI

(Wenn du die Aufgabe alleine rechnest, kannst du natürlich auch eine der anderen beiden Lösungen als erratene Lösung verwenden. Dann ergibt sich zwar eine andere zweite Polynomdivision und eine andere quadratische Gleichung. Doch letztendlich wirst du, wenn du richtig rechnest, zu den gleichen Ergebnissen kommen, nur in einer anderen Reihenfolge.) Da die erratene Lösung 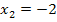ist, muss 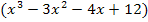durch den Faktor 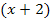geteilt werden.

2. Polynomdivision

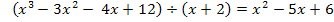
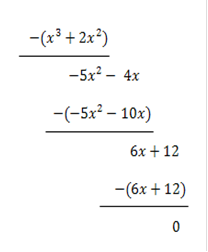
Das Ergebnis dieser Polynomdivision wird wieder gleich Null gesetzt.

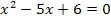
Nun liegt eine gemischtquadratische Gleichung vor. Sie kann entweder mit der Mitternachtsformel oder mit dem Satz von Vietagelöst werden. (Eine binomische Formel liegt nicht vor.) Wir entscheiden uns hier für die Mitternachtsformel, obwohl das etwas länger dauert als mit dem Satz von Vieta. Aber die meisten Schüler bevorzugen die Mitternachtsformel, daher verwenden wir diesen Weg.

Hier noch einmal die Mitternachtsformel:

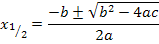
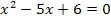
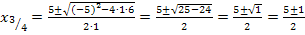
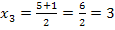
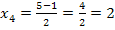
Damit sind alle Nullstellen von F berechnet.

F besitzt 4 einfache Nullstellen bei 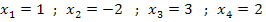. Bei jeder Nullstelle schneidet der Graph von F die x-Achse.

Ein anderer Aufgabentyp, der gerne in Prüfungen verlangt wird, kommt ohne konkrete Rechnung aus. Es ist ausschließlich der Graph einer Funktion zu verwenden, um den Graph 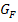einer Integralfunktion 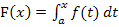zu beschreiben oder grob zu skizzieren. Schauen wir uns so eine Aufgabe gleich einmal an.

9. Bsp.:In der folgenden Abbildung ist der Graph 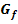einer Funktion 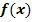dargestellt. Alle Nullstellen sind ganzzahlig. Der relative Hochpunkt von 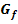liegt bei 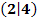. Außerdem ist bekannt: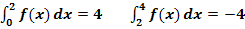

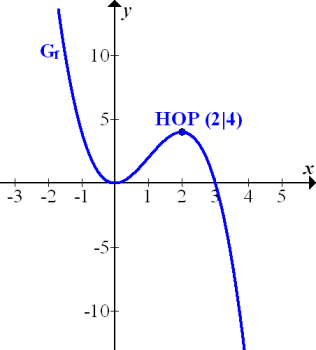
Abb.:Graph

Wir betrachten nun die Integralfunktion .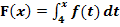

Welche Eigenschaften von F kann man aus 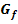folgern? Beantworte dabei insbesondere folgende Fragen:

Was lässt sich über die Anzahl und Lage der Nullstellen von F sagen? (Beachte dabei auch die angegebenen bestimmten Integrale!)

Was kann man bezüglich Monotonie- und Krümmungsverhalten von F aus 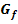folgern? Besitzt der Graph von F ein Extremum? Hat F einen Terrassenpunkt? Wenn ja, welche Koordinaten hat er? Gibt es bei F Wendepunkte und wo liegen diese? Welche Steigung besitzt die Wendetangente?

Skizziere den Graph von F!

Lösung:

Nullstellen von F:

Die Integralfunktion 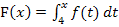hat als untere Grenze die Zahl 4. Daher muss F bei 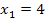auf jeden Fall eine Nullstelle besitzen. Das Integral 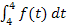muss schließlich Null ergeben, da obere und untere Grenze zusammenfallen. Daher gilt: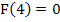

Die erste Nullstelle bei 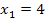ist somit schon bekannt.

---