Die Integralfunktion und der HDI
Die Funktion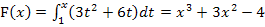 
besitzt daher zwei verschiedene Nullstellen:Eine einfache Nullstelle bei 
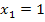und eine doppelte Nullstelle bei 
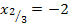. Bei der einfachen Nullstelle schneidet der Graph von F die x-Achse, bei der doppelten Nullstelle berührt er die x-Achse nur, schneidet sie also nicht. (Siehe auch:Vielfachheiten der Nullstellen) Dass sich sowohl bei Teilaufgabe 8a. als auch bei 8b. eine einfache Nullstelle bei der unteren Grenze und eine doppelte an einer anderen Stelle ergeben hat, war reiner Zufall. Das ist nicht immer so!
Zu 8c.)
Hier noch einmal die Angabe: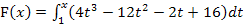 
1. Schritt:Integralfreie Darstellung von F ermitteln, d.h. Integral ausrechnen
Um eine Stammfunktion, d.h. den Ausdruck in der eckigen Klammer, zu bekommen, muss zu jeder Potenz von t der Exponent um 1 erhöht werden und außerdem durch diejenige Zahl geteilt werden, die nun im Exponenten steht. Bei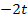 
steht zwar kein Exponent beim t;dabei denkst du dir einfach den Exponenten 1 dazu. Bei der Zahl +16 ergänzt du in Gedanken 
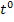, falls du Probleme beim Integrieren hast.
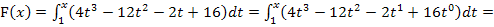
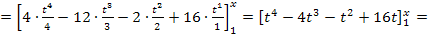
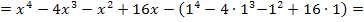
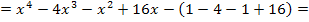
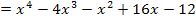
Somit wissen wir: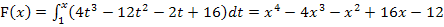 
2. Schritt:Nullstellenberechnung von F, d.h. integralfreie Darstellung gleich Null setzen
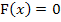
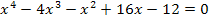
Nun liegt eine Gleichung vierten Grades vor. Wir müssen insgesamt zwei Polynomdivisionen durchführen, bis wir auf eine Gleichung zweiten Grades kommen, die man leicht nach x auflösen kann. Die erste Lösung der Gleichung kennen wir;sie stimmt schließlich mit der unteren Grenze überein. Die erste Nullstelle von F liegt bei .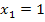
Wir teilen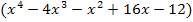 
durch den Faktor 
.
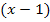1. Polynomdivision
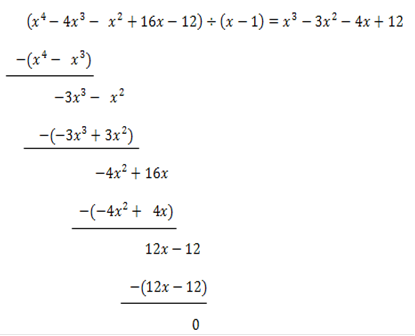
Das Ergebnis dieser Polynomdivision setzen wir gleich Null.
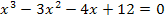
Es liegt nun eine Gleichung dritten Grades vor. Wir müssen noch eine Polynomdivision durchführen. Allerdings muss nun eine weitere Lösung erraten werden. Wenn du mit dem Taschenrechner eine Wertetabelle von -3 bis 3 mit der Schrittweite △x = 1 erstellst, wirst du direkt auf alle drei Lösungen dieser Gleichung stoßen: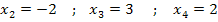 
Bekanntlich kann eine Gleichung dritten Grades maximal drei Lösungen besitzen. Wir kennen also bereits alle Lösungen. Allerdings darfst du nur eine dieser Lösungen durch Ausprobieren bzw. Raten finden;die anderen beiden müssen wirklich berechnet werden. Sonst gibt es in Prüfungen nicht die volle Punktzahl! Welche der drei soeben aufgeführten Lösungen als erratene Lösung betrachtet wird, ist egal. Wir wählen hier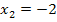 
.
