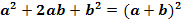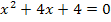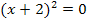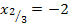Die Integralfunktion und der HDI
Bei der einfachen Nullstelle schneidet der Graph von F die x-Achse, bei der doppelten Nullstelle berührt er die x-Achse nur, schneidet sie also nicht. (Siehe auch:Vielfachheiten der Nullstellen)
Zu 8b.)
Hier noch einmal die Angabe: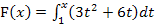 
1. Schritt:Integralfreie Darstellung von F ermitteln, d.h. Integral ausrechnen
Um eine Stammfunktion, d.h. den Ausdruck in der eckigen Klammer, zu bekommen, muss zu jeder Potenz von t der Exponent um 1 erhöht werden und außerdem durch diejenige Zahl geteilt werden, die nun im Exponenten steht. Bei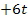 
steht zwar kein Exponent beim t;dabei denkst du dir einfach den Exponenten 1 dazu.
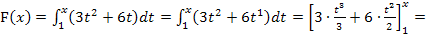
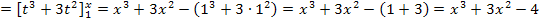
Somit wissen wir: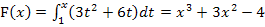 
2. Schritt:Nullstellenberechnung von F, d.h. integralfreie Darstellung gleich Null setzen
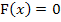
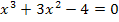
Nun ist, wie schon in der Teilaufgabe 8a, eine Gleichung dritten Grades zu lösen. Es wieder eine Polynomdivision nötig, da das Ausklammern von x wegen der Konstanten – 4 nichts bringt. Wir brauchen die erste Lösung nicht erraten, den wir wissen, dass jede Integralfunktion bei ihrer unteren Grenze eine Nullstelle besitzt. Die untere Grenze ist in diesem Fall die Zahl 1;somit hat F bei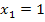 
sicher eine Nullstelle.
Nun dividieren wir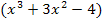 
durch 
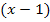. Auf die Zahl – 1 in der Klammer kommt man durch Umdrehen des Vorzeichens der ersten Lösung 
.
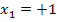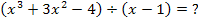
Bei dem Ausdruck in der vorderen Klammer fehlt die Potenz x bzw.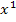 
. Damit du die Polynomdivision leichter ausrechnen kannst, solltest du den Term 
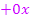ergänzen. Jetzt versuche es doch gleich mal selbst, bevor du dir den Rest der Lösung ansiehst!
Polynomdivision:
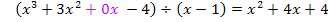
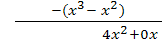
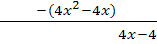
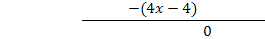
Jetzt muss nur noch das Ergebnis der Polynomdivision gleich Null gesetzt und nach x aufgelöst werden.
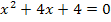
Du kannst nun entweder die Mitternachtsformel anwenden oder in diesem Fall mit der ersten binomischen Formel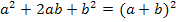 
arbeiten. (Eine binomische Formel kann natürlich nicht bei jeder quadratischen Gleichung angewendet werden. Du musst selbst überlegen, ob es funktioniert oder nicht. Die Mitternachtsformel klappt dagegen bei allen Gleichungen der Form 
.)
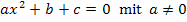1. Lösungsweg:Mit Mitternachtsformel
Zur Erinnerung:
Gleichungen der Form 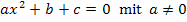werden mit der folgenden Formel nach x aufgelöst:
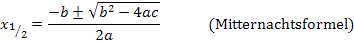
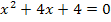
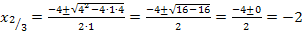
Es liegt eine doppelte Nullstelle bei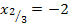 
vor.
Anmerkung:Die Bezeichnung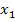 
ist bereits für die erste Nullstelle 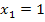(vgl. untere Grenze) vergeben. Daher wird für die andere Nullstelle die Bezeichnung 
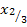verwendet.
2. Lösungsweg:Mit der ersten binomischen Formel 
