Die Integralfunktion und der HDI

Dazu muss normalerweise eine Lösung erraten werden, weil man dabei schließlich durch (x – erste Lösung) dividiert. Das Erraten der ersten Lösung ist hier aber gar nicht nötig! Die erste Lösung lässt sich nämlich ganz bequem an der unteren Grenze von F ablesen. Wir wissen, dass eine der Nullstellen einer Integralfunktion F grundsätzlich mit der unteren Grenze von F übereinstimmt.

Die untere Grenze von 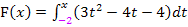liegt bei – 2;die erste Nullstelle und somit erste Lösung unserer Gleichung ist 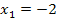. Das Integral von -2 bis -2 ist ja zwangsläufig gleich Null;da ist logischerweise keine Fläche.

Erste Lösung, vgl. untere Grenze: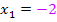

Polynomdivision:

Wir teilen nun den Ausdruck 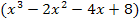durch den Faktor 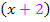. Beachte, dass das Vorzeichen genau umgekehrt ist im Vergleich zur ersten Lösung!

Merke:Du musst bei der Polynomdivision immer durch 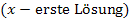dividieren! Das Minus-Zeichen in der Klammer führt dazu, dass sich das Vorzeichen im Vergleich zur ersten Lösung umdreht. In der Klammer, durch die dividiert wird, steht daher hinter dem x immer die erste Lösung nur mit umgedrehtem Vorzeichen.

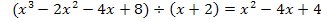
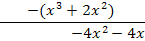
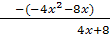
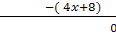
Die Polynomdivision muss aufgehen! Wenn das nicht der Fall ist, hast du dich verrechnet! Kontrolliere dann noch einmal deine Vorzeichen. Meist kommt es vor allem beim Abziehen von negativen Zahlen zu Fehlern.

Das Ergebnis der Polynomdivision muss wieder gleich Null gesetzt werden.

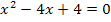
Dies ist eine gemischtquadratische Gleichung, d.h. eine Gleichung mit 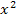und x. Solche Gleichungen können auf jeden Fall mit der Mitternachtsformel gelöst werden. Manchmal kann stattdessen auch eine binomische Formelangewendet werden, so wie auch in diesem Beispiel. Wenn du die binomische Formel erkennst, kommst du etwas schneller zur Lösung als mit der Mitternachtsformel. Ohne binomische Formel geht´s natürlich trotzdem:Wie bereits gesagt:Einfach die Mitternachtsformel anwenden. Das ist für viele Schüler leichter. Es werden im Folgenden beide Lösungswege gezeigt. Du kannst dir dann denjenigen heraussuchen, der dir besser liegt.

1. Lösungsweg:Mit Mitternachtsformel

Zur Erinnerung:

Gleichungen der Form 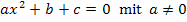werden mit der folgenden Formel nach x aufgelöst:

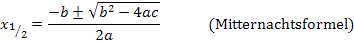
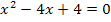
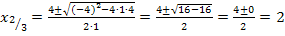
Es liegt eine doppelte Nullstelle bei 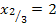vor.

Anmerkung:Die Bezeichnung 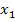ist bereits für die erste Nullstelle 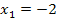(vgl. untere Grenze) vergeben. Daher wird für die andere Nullstelle die Bezeichnung 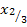verwendet.

2. Lösungsweg:Mit der zweiten binomischen Formel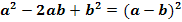

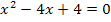
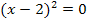
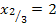
Die Funktion 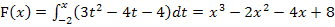besitzt daher zwei verschiedene Nullstellen:Eine einfache Nullstelle bei 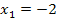und eine doppelte Nullstelle bei .

---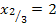