Die Integralfunktion und der HDI
In diesem Beispiel haben wir nur an Hand des Graphen von f die Anzahl und (ungefähre) Lage der Nullstellen der Integralfunktionen F und G erschlossen. Natürlich kann man die Nullstellen einer Integralfunktion auch rechnerisch ermitteln. Das geht allerdings nur dann, wenn man F integralfrei darstellen kann, d.h. wenn man das Integral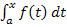 
ausrechnen kann. Das klappt wiederum nur, wenn eine Stammfunktion zu f ermittelt werden kann. Im nächsten Beispiel kannst du sehen, wie sich die Nullstellen einer Integralfunktion berechnen lassen. Ohne integralfreie Darstellung können die Nullstellen einer Integralfunktion nicht berechnet werden – außer es gibt nur eine einzige Nullstelle, diese entspricht bekanntlich der unteren Grenze. Dazu muss man nichts rechnen. Die Kenntnis dieser ersten Nullstelle von F ist wichtig, denn oftmals hilft dies bei der Berechnung der weiteren Nullstellen. Warum? Das siehst du jetzt gleich am nächsten Beispiel.
8. Bsp.:Berechne alle Nullstellen der folgenden Integralfunktionen!
a.)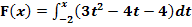 
b.)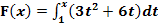 
c.)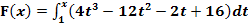 
Lösung:
Um alle Nullstellen einer Integralfunktion zu berechnen, muss vorweg die integralfreie Darstellung der jeweiligen Integralfunktion F ermittelt werden. Diese wird dann gleich Null gesetzt und nach x aufgelöst. Ist dabei eine Gleichung höher als zweiten Grades (d.h. eine Gleichung mit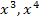 
oder einer noch höheren Potenz von x) zu lösen, bei der eine Polynomdivision nötig ist, muss die erste Lösung nicht erraten werden! Die erste Nullstelle ist durch die untere Grenze von F bestimmt und somit schon bekannt!
Zu 8a.)
1. Schritt:Integralfreie Darstellung von F ermitteln, d.h. Integral ausrechnen
Um eine Stammfunktion, d.h. den Ausdruck in der eckigen Klammer, zu bekommen, muss zu jeder Potenz von t der Exponent um 1 erhöht werden und außerdem durch diejenige Zahl geteilt werden, die nun im Exponenten steht. Bei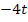 
steht zwar kein Exponent beim t;dabei denkst du dir einfach den Exponenten 1 dazu. Bei der Zahl -4 denkst du dir ein t mit dem Exponenten Null dazu.
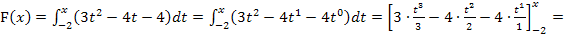
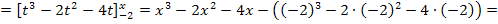
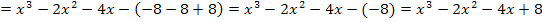
Somit wissen wir: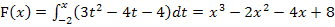 
2. Schritt:Nullstellenberechnung von F, d.h. integralfreie Darstellung gleich Null setzen
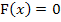
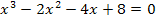
Nun liegt eine Gleichung dritten Grades vor, weil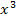 
die höchste auftretende Potenz ist. Wegen der Konstanten + 8 bringt uns das Ausklammern von x nicht weiter. (Ausführlichere Erklärungen im Kapitel Gleichungen dritten und höheren Grades) Wir müssen eine Polynomdivision durchführen.
