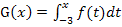Die Integralfunktion und der HDI
Am Ende der Lösung von Teilaufgabe 7c.) ist auch der Graph von F dargestellt.
Zu 7c.)
Die Integralfunktion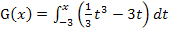 
unterscheidet sich nur in ihrer unteren Grenze von der Integralfunktion 
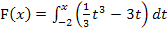. Sowohl G als auch F sind Integralfunktionen zur gleichen Funktion 
. Daher geht der Graph der Funktion G zwangsläufig durch Verschiebung nach oben / unten entlang der y-Achse aus dem Graph von F hervor. (Ob eine Verschiebung nach oben oder unten vorliegt, müssten wir uns noch überlegen.) Durch die Änderung der unteren Grenze ändert sich auf diesem Fall die Anzahl der Nullstellen im Vergleich zu F.
Überlegen wir uns nun die Nullstellen von 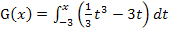. Die erste Nullstelle liegt bei der unteren Grenze von G, also bei x = -3. Das ist klar, doch gibt es noch weitere Nullstellen von G? Um diese Frage beantworten zu können, brauchen wir wieder den Graph von 
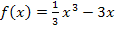. Hier noch einmal der Graph 
:
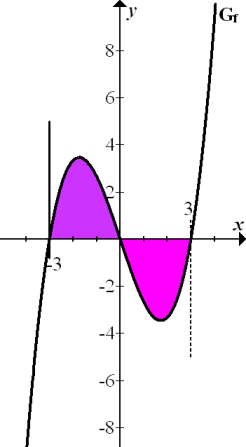
Die untere Grenze der Integralfunktion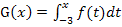 
liegt bei x = -3. Daher müssen wir uns überlegen, für welche Werte von x das Integral (also die Flächenbilanz) Null ergibt, wenn wir bei x = -3 beginnen. (Die senkrechte Gerade x = -3 ist in der obigen Abbildung fett eingezeichnet, um zu symbolisieren, dass dort die untere Grenze der Integralfunktion G liegt.) Auf Grund der Punksymmetrie des Graphen ist es klar, dass die lilafarbene Fläche genauso großist wie die rosafarbene. Wir integrieren von x = -3 ab nach rechts, also in die „richtige Richtung“. Das lilafarbene Flächenstück von x = -3 bis x = 0 liegt oberhalb der x-Achse;es geht positiv in die Flächenbilanz ein. Das rosafarbene Flächenstück von x = 0 bis x = 3 liegt unterhalb der x-Achse;es geht negativ in die Flächenbilanz ein. Weil beide Flächenstücke gleich großsind, heben sie sich in der Flächenbilanz gegenseitig auf und die Flächenbilanz von -3 bis 3 ergibt 0. Daher ist auch das Integral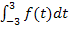 
gleich 0 und die Integralfunktion 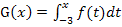hat bei x = 3 eine weitere Nullstelle. Andere Flächenstücke, die sich in der Flächenbilanz aufheben würden, weil sie gleich großsind, aber einmal oberhalb und einmal unterhalb der x-Achse liegen gibt es nicht. Zumindest nicht, wenn wir von x = -3 (untere Grenze von G) ausgehen. Deshalb hat G sonst keine weiteren Nullstellen.
Die Integralfunktion 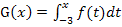hat somit nur zwei Nullstellen. Sie liegen bei:
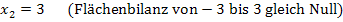
In der nächsten Abbildung kannst du die Graphen von f, F und G in einem gemeinsamen Koordinatensystem sehen. Der Graph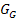 
geht durch eine Verschiebung nach oben aus dem Graph 
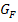hervor.
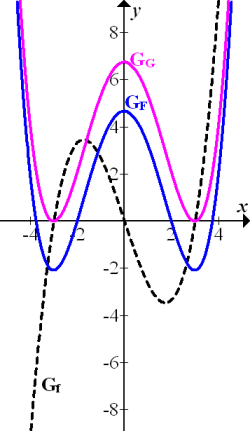
Abb.:Graph der Funktion 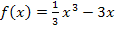mit den Graphen 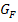und 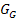der beiden Integralfunktionen 
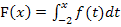und
