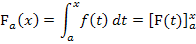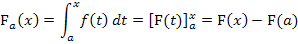Die Integralfunktion und der HDI
Dass als Variable u oder a vorkommt, ist jedoch wirklich die Ausnahme und soll bloßzur Verwirrung der Schüler beitragen. Wir bleiben auf dieser website immer bei der Bezeichnung x für die Variable, solange es um Integralfunktionen geht.
Eine Integralfunktion hat eine konkrete, feste Grenze (in der Regel die untere) und eine variable Grenze (normalerweise x als obere Grenze). Bei einer Integralfunktion ist also die eine Grenze eine Zahl, die andere immer ein variabler Buchstabe.
Unterscheide genau zwischen bestimmten Integral, unbestimmten Integral und Integralfunktion! Im Gegensatz zur Integralfunktion sind beim bestimmten Integral beide Grenzen konkrete Zahlen. Ein unbestimmtes Integral hat dagegen gar keine Grenzen.
Unbestimmtes Integral (Menge aller Stammfunktionen):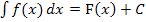 
Bestimmtes Integral (Flächenbilanz): Integralfunktion (Flächenbilanzfunktion): |
Die Grenzen einer Integralfunktion sind also a und x. Dabei stellt a eine feste Zahl dar, mit a 
ℝ. Die untere Grenze a liegt fest, während die obere Grenze x variabel ist.
Weil hierbei „ x “ schon die Bezeichnung für die obere Grenze ist, kann nicht mehr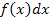 
hinter das Integral geschrieben werden. Die Bezeichnung „ x “ ist quasi schon für die obere Grenze vergeben. Man verwendet daher statt 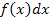bei einer Integralfunktion immer 
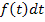. Warum gerade 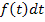und nicht zum Beispiel 
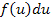oder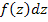 
lässt sich nicht genau sagen;das ist einfach so gewählt worden. Man hätte auch jeden anderen Buchstaben außer der Bezeichnung der Variablen selbst nehmen können. 
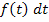ist eben üblich.
Integralfreie Darstellung einer Integralfunktion
Wenn man das Integral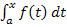 
ausrechnet, erhält man die sogenannte integralfreie Darstellung der Integralfunktion.
Aber wie rechnet man eine Integralfunktion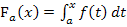 
aus? Das funktioniert im Prinzip genauso wie beim bestimmten Integral. Mathematisch korrekt sagt man aber nicht „Integralfunktion ausrechnen“, sondern „integralfrei darstellen“. Wenn in einer Aufgabe steht, dass du eine Integralfunktion integralfrei schreiben sollst oder ihre integralfreie Darstellung finden sollst, dann ist damit nichts anderes gemeint, als dass du das Integral 
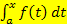ausrechnen sollst.
| Integralfreie Darstellung einer Integralfunktion ermitteln:
1. Schritt:Stammfunktion zu Das t entspricht dabei dem x aus dem bestimmten Integral Die Stammfunktion
2. Schritt:Grenzen einsetzen Zuerst wird die obere Grenze, also x, für jedes vorkommende t in die Stammfunktion eingesetzt. (Daher konnte auch nicht x bei der Stammfunktion verwendet werden, denn man kann schließlich nicht x für x einsetzen.) Dann muss außerdem die untere Grenze a für jedes in der Stammfunktion auftretende t eingesetzt werden und von dem Ausdruck abgezogen werden, der sich durch das Einsetzen der oberen Grenze ergeben hat. Merke: Immer obere Grenze minus untere Grenze! Nicht umgekehrt!
|
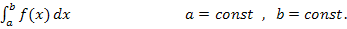
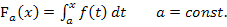
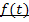
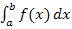. (Wir integrieren ja momentan nach t und nicht nach x.) Eine kurze Zusammenfassung der wichtigsten Integrationsregeln findest du bei 
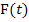schreibt man in eckige Klammern, so wie beim bestimmten Integral. Die Grenzen werden ebenfalls oben und unten an die rechte Klammer geschrieben, nur dass jetzt x die obere Grenze ist. Das „ + C “ kann dabei, wie beim bestimmten Integral, weggelassen werden. (Nur beim unbestimmten Integral, also wenn das Integral keine Grenzen hat, muss „ + C “ dazu geschrieben werden.)
