Die Integralfunktion und der HDI
Die Funktion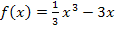 
schneidet bei x = – 3 die x-Achse. Das wurde hier nur aus der Zeichnung abgelesen;du kannst das aber leicht rechnerisch überprüfen:
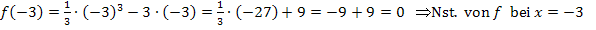
Geht man von x = – 3 weiter nach links bis ungefähr x = – 3,8 , dann wird die Fläche zwischen 
und der x-Achse (in der Abbildung rot markiert) genauso groß, wie die Fläche zwischen und der x-Achse von x = – 2 bis x = – 3 (orange markiert). Die rote und die orangefarbene Fläche sind jeweils gleich groß. Die eine liegt oberhalb der x-Achse, die andere liegt unterhalb. Die Flächenbilanz wird daher gleich Null und F hat bei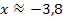 
eine weitere Nullstelle.
Zu beachten ist hier außerdem, dass man in die „falsche“ Richtung integriert, d.h. von rechts nach links! Du weißt:Vertauscht man die Grenzen eines bestimmten Integrals, so ändert sich das Vorzeichen des Integrals. Daher zählen bei der Integration von rechts nach links, Flächenstücke oberhalb der x-Achse negativ und Flächenstücke unterhalb der x-Achse entsprechend positiv.
Achtung:Du musst hier immer bei x = – 2 beginnen, da dies die untere Grenze der Integralfunktion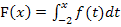 
ist. Wenn du also zu Zahlen gehst, die links von -2 liegen, wird die obere Grenze kleiner als die untere und du integrierst zwangsläufig in die „falsche“ Richtung!
Die Fläche von x = – 2 bis x = – 3 (orange markiert) liegt oberhalb der x-Achse. Man integriert allerdings in die „falsche“ Richtung, also von der größeren Zahl (untere Grenze -2) zur kleineren Zahl (obere Grenze -3), somit ergibt sich für das Integral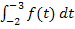 
ein negativer Wert. Die orange Fläche geht hier negativ in die Flächenbilanz ein, obwohl sie oberhalb der x-Achse liegt.
Wenn man nun von x = – 3 noch weiter nach links geht, bekommt man eine Fläche, die vollständig unterhalb der x-Achse liegt. (Rot markierte Fläche) Wegen der „falschen“ Integrationsrichtung wird dieses Flächenstück positiv gezählt. (Sowohl -3 als auch -3,8 liegen schließlich links von der unteren Grenze -2. Deshalb immer noch „falsche“ Integrationsrichtung!) Das rot markierte Flächenstück geht daher positiv in die Flächenbilanz ein, obwohl es unterhalb der x-Achse liegt.
Wir fassen zusammen:Das orange markierte Flächenstück liegt oberhalb der x-Achse und das rote Flächenstück unterhalb der x-Achse. Da beide Flächenstücke gleich großsind und das eine negativ und das andere positiv gezählt wird, ist die Flächenbilanz gleich Null. Es gilt: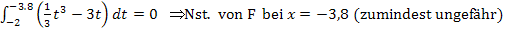 
Andere Flächenstücke, die sich gegenseitig aufheben, gibt es hier nicht. Daher gibt es auch keine weiteren Nullstellen von F.
