Die Integralfunktion und der HDI
Geht man von x = – 2 bis ungefähr x = – 3,8 dann ist das der Fall und außerdem noch bei ungefähr x = 3,8.Weitere Möglichkeiten gibt es nicht. Daher hat F genau 4 Nullstellen:
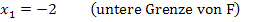
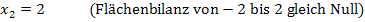
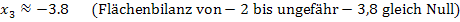
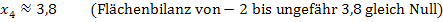
Falls dir das nicht ganz klar ist, betrachte dazu die nächste Abbildung. Ausführliche Erklärungen zu den einzelnen Nullstellen folgen gleich etwas weiter unten.
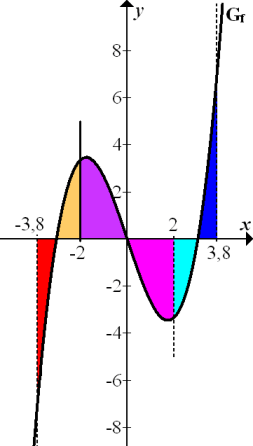
Abb.:Zur Flächenbilanz der Funktion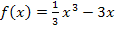 
Die senkrechte Gerade x = -2 ist fett eingezeichnet, um zu symbolisieren, dass es sich dabei um die untere Grenze der Integralfunktion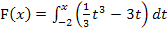 
handelt. Wir starten in Gedanken immer bei der unteren Grenze x = -2, wenn wir uns die Flächenbilanz F zu 
überlegen.
Die rote Fläche ist genauso großwie die orangefarbene Fläche. Die lila Fläche ist genauso großwie die rosa Fläche. Außerdem ist die hellblaue Fläche genauso großwie die dunkelblaue.
Ausführliche Erklärungen zur Nullstelle von F bei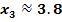 
In der obigen Abbildung ist zu erkennen, dass die lilafarbene Fläche und die rosafarbene Fläche gleich großsind, ebenso die hellblaue Fläche und die dunkelblaue. Die lila Fläche liegt oberhalb der x-Achse, die rosa markierte unterhalb. Diese beiden Flächen heben sich gegenseitig in der Flächenbilanz auf. Entsprechendes gilt für die hellblaue und die dunkelblaue Fläche.
Die hellblau markierte Fläche geht von x = 2 bis x = 3. Der linke Rand der hellblauen Fläche x = 2 entspricht dem rechten Rand der rosafarbenen Fläche. Der Wert x = 2 hat sich aus der Überlegung ergeben, dass sich die lilafarbene mit der rosafarbenen Fläche aufheben muss. Der rechte Rand der hellblauen Fläche entspricht der positiven Nullstelle von 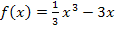. Aus der Zeichnung lesen wir ab, dass sie bei x = 3 liegt. Das kannst du leicht rechnerisch kontrollieren: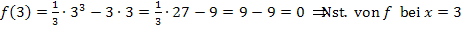 
Der linke Rand der dunkelblauen Fläche entspricht dem rechten Rand der hellblau markierten. Die dunkelblaue Fläche beginnt also bei x = 3.Wo der rechte Rand der dunkelblauen Fläche ist, lässt sich nur grob abschätzen. Wir haben hier den Wert x = 3,8 verwendet. Das ist aber nur eine ganz grobe Schätzung.
Die beiden oberhalb der x-Achse liegenden Flächenstücke (lila von x = – 2 bis x = 0 und dunkelblau von x = 3 bis ungefähr x = 3.8) sind zusammen genauso großwie die beiden unterhalb der x-Achse liegenden Flächenstücke (rosa von x = 0 bis x = 2 und hellblau von x = 2 bis x = 3) Die Flächenbilanz von -2 bis ungefähr 3,8 ergibt den Wert Null.
Das Integral von -2 bis ungefähr 3.8 muss daher gleich Null sein und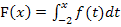 
hat bei 
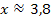eine weitere Nullstelle.
Ausführliche Erklärungen zur Nullstelle von F bei 
