Die Integralfunktion und der HDI
c.) Zum Vergleich betrachten wir nun auch die Funktion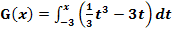 
. Die Funktion G unterscheidet sich nur in der unteren Grenze von 
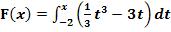. Wie viele Nullstellen hat G? Wo liegen sie? Wie wirkt sich eine Veränderung der unteren Grenze auf den Graph einer Integralfunktion aus?
Lösung:
Zu 7a.)
Die Funktion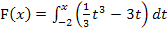 
ist eine Integralfunktion, weil die Variable x die obere Grenze bildet. Jede Integralfunktion hat bei ihrer unteren Grenze eine Nullstelle. Ob es noch weitere Nullstellen gibt, lässt sich allgemein nicht sagen. Eine Integralfunktion hat auf jeden Fall mindestens eine Nullstelle, nämlich bei ihrer unteren Grenze.
Weil F eine Integralfunktion ist, hat F sicher mindestens eine Nullstelle. Diese Nullstelle liegt bei x = – 2, da die untere Grenze – 2 ist. Das Integral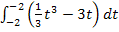 
muss schließlich gleich Null sein, denn es gibt keine Fläche von x = – 2 (untere Grenze) bis x = – 2 (obere Grenze) zwischen 
und der x-Achse. Sind obere und untere Grenze identisch, ist ein Integral deswegen immer gleich Null.
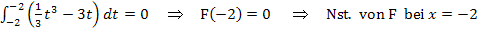
Zu 7b.)
Es soll nun die Anzahl der Nullstellen von 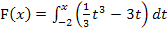ohne Rechnung nur mit Hilfe des Graphen der Integrandenfunktion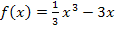 
ermittelt werden. Wie geht das? Hm?
Du weißt:Bei einer Nullstelle von F muss gelten:
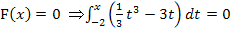
Du musst also herausfinden, für welchen Wert von x das Integral Null ergibt. Die erste Nullstelle kennen wir schon:Sie liegt bei der unteren Grenze:x = -2
Doch wo liegen eventuell weitere Nullstellen? Das Integral entspricht bekanntlich der Flächenbilanz. Du musst dich daher fragen, für welche Werte von x die Flächenbilanz gleich Null wird, wenn du die Nullstellen einer Integralfunktion F suchst.
Flächenstücke zwischen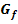 
und der x-Achse, die oberhalb der x-Achse liegen, werden bei der Flächenbilanz positiv gezählt. Das gilt aber nur, wenn man von der kleineren zur größeren Zahl integriert, d.h. wenn die untere Grenze kleiner ist als die obere. Flächenstücke unterhalb der x-Achse werden bei der Flächenbilanz negativ gezählt, zumindest dann wenn man von der kleineren zur größeren Zahl integriert, d.h. wenn die untere Grenze kleiner ist als die obere. Integriert man in die andere Richtung, also von der größeren Zahl (untere Grenze) zur kleineren Zahl (obere Grenze), ist es genau umgekehrt. Dann werden Flächenstücke oberhalb der x-Achse negativ gezählt und Flächenstücke unterhalb der x-Achse positiv. Das wird hier noch wichtig, denn die obere Grenze x kann schließlich auch Werte annehmen, die kleiner sind als die untere Grenze – 2. Aber egal, in welche Richtung integriert wird:Die Flächenbilanz und somit das Integral ist gleich Null, wenn die Flächenstücke oberhalb der x-Achse zusammen genauso großsind wie die unterhalb.
Entscheidend ist dabei jedoch, von wo man losgeht, also wo die untere Grenze des Integrals liegt.
