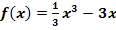Die Integralfunktion und der HDI

Erstens wäre das unnötiger Arbeitsaufwand und zweitens steht extra in der Aufgabenstellung, dass ohne Verwendung der integralfreien Form von F gerechnet werden soll. Du darfst momentan also noch gar nicht integrieren! Du sollst einfach den HDI verwenden, welcher besagt:F´(x) = f (x)

Hier noch einmal die Gleichung von F:

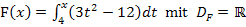
Laut HDI gilt: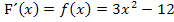

Extrema von F: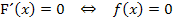

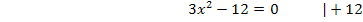
Die Art der Extrema kann man entweder mit Hilfe der Monotonie von F oder mit Hilfe der zweiten Ableitung von F ermitteln. Solltest du die Zweite Ableitungim Unterricht noch nicht behandelt haben, verwendest du zwangsläufig die Monotonieuntersuchung von F. In diesem Fall bietet es sich jedoch an, die Art der Extrema mit Hilfe der zweiten Ableitung von F zu ermitteln.

Art der Extrema mit F´´(x) ermitteln:

Laut HDI gilt: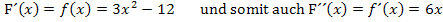

Wir setzen jeweils die x-Koordinaten der Extrema in F´´(x) ein und ermitteln das Vorzeichen der Ergebnisse.

Zur Erinnerung:Ist die zweite Ableitung negativ, ist der Graph rechtsgekrümmt und es liegt ein Hochpunkt vor. Ist die zweite Ableitung positiv, ist der Graph der Funktion linksgekrümmt und es handelt sich um einen Tiefpunkt.

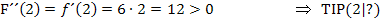
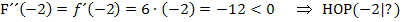
Integralfreie Darstellung von 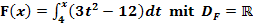ermitteln:

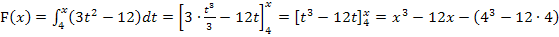
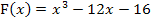
Berechnung der y-Koordinaten der Extrempunkte von F:

Wir müssen die y-Koordinaten der Extrema von F berechnen und nicht etwa die von f. Es gilt hier:y = F(x)

Deshalb setzen wir die berechneten x-Koordinaten der Extrema nun in 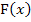ein und nicht in .

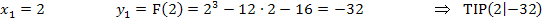
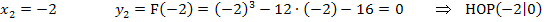
Fertig!

In den folgenden Aufgabenbeispielen wollen wir uns mit dem Thema „Nullstellen einer Integralfunktion“ beschäftigen. Wie wir schon besprochen haben, hat jede Integralfunktion mindestens eine Nullstelle, nämlich genau bei ihrer unteren Grenze. Jetzt stellt sich die Frage, ob es denn bei einer bestimmten Integralfunktion noch weitere Nullstellen gibt, und wo diese liegen, falls es weitere gibt. Diese Frage kann nur im speziellen Fall beantwortet werden;das hängt nämlich ganz von der Integrandenfunktion und der jeweiligen unteren Grenze von F ab.

7. Bsp.:

Wir betrachten die Funktion .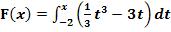

a.) Begründe, warum die Funktion F mindestens eine Nullstelle besitzt! Gib diese Nullstelle an.

b.) Gegeben ist nun auch der Graph 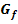der Funktion 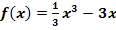. Siehe Abbildung! Bestimme nur mit Hilfe des Graphen die Anzahl der Nullstellen von F und gib eine weitere Nullstelle von F exakt an! Wo liegen die restlichen Nullstellen ungefähr? (Grobe Schätzung reicht, keine Rechnung)

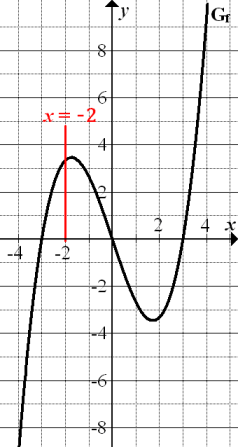
Abb.:Graph der Funktion

---