Die Integralfunktion und der HDI

)

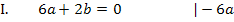
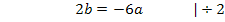
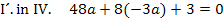
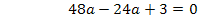
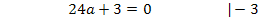
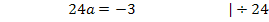
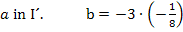
2. Methode:Additionsverfahren

Hier noch einmal die beiden Gleichungen:

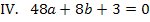
Um b zu eliminieren, multiplizieren wir Gleichung I. mit dem Faktor 4 und ziehen davon Gleichung II. ab. Dir ist nicht klar, warum I. genau mit 4 multipliziert werden muss? Ganz einfach:Wenn man I. mit 4 multipliziert, kommt auch in der ersten Gleichung 8b vor, wie schon in IV. Zieht man diese beiden Gleichungen voneinander ab, fällt die Unbekannte b komplett heraus. Es entsteht dadurch eine Gleichung, die nur noch die Unbekannte a enthält, die dann leicht ausgerechnet werden kann. Nachdem man a ermittelt hat, kann der berechnete Wert für a in eine der Gleichungen I. oder IV. eingesetzt und dann b berechnet werden.

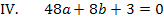
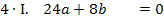
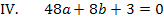
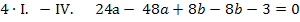
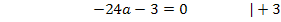
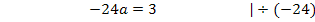
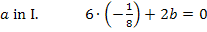
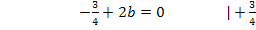
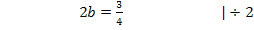
Nun sind alle drei Koeffizienten ermittelt: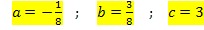

Wir müssen sie nur noch in 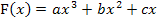einsetzen. So erhalten wir das gesuchte Ergebnis: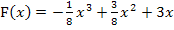

6. Bsp.:

Gegeben ist die Funktion 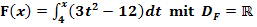. Ihr Graph sei mit 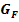bezeichnet.

Ermittle die Abszissen und die Art der Extrema von F ohne Verwendung der integralfreien Darstellung von F! Gib sodann die integralfreie Darstellung von F an und berechne die Ordinaten der Extrema!

Lösung:

Du kannst mit den Begriffen „Abszisse“ und „Ordinate“ nichts anfangen? Kein Problem! Die Abszisse eines Punktes ist nichts anderes als seine x-Koordinate. Die Ordinate ist die y-Koordinate des Punktes. Du sollst in dieser Aufgabe also zuerst bloßdie x-Koordinaten der Extrema von F ausrechen, aber ohne dabei das Integral auszurechnen. (Es ist ja extra verlangt, die Abszissen und die Art der Extrema von F ohne integralfreie Darstellung zu ermitteln.) Erst nachher soll die integralfreie Darstellung von F berechnet werden. (Nun sollst du das Integral wirklich ausrechnen.) Damit lassen sich dann auch die y-Koordinaten der Extrema von F ausrechnen.

Berechnung der Abszisse der Extrema von F

Bei einem Extremum verläuft die Tangente an den Funktionsgraph bekanntlich waagrecht. Die Steigung der Tangente, d.h. die erste Ableitung der Funktion, muss daher bei einem Extrempunkt gleich Null sein. Wir suchen hier die Extrema von F und nicht etwa von f. Daher muss die erste Ableitung von F gleich Null gesetzt werden. Um F´(x) zu bilden, nimmst du einfach . Also nicht zuerst integrieren und dann wieder ableiten!

---