Die Integralfunktion und der HDI
Die integralfreie Darstellung würde dabei erst ermittelt werden, nachdem die Koeffizienten a, b und c berechnet wurden.
Nun stellen wir drei Gleichungen für die drei Unbekannten a, b und c auf. Man braucht schließlich immer genauso viele Gleichungen wie Unbekannte, um die Unbekannten berechnen zu können.
Hier noch einmal die entscheidenden Angaben:Wendepunkt von F bei x = 1, Extremum von F an der Stelle x = 4 und die Steigung 3 der Funktion F bei x = 0
Die erste Gleichung ergibt sich aus der Information „F hat einen Wendepunkt bei x = 1“. Bei Wendepunkten ist die zweite Ableitung bekanntlich gleich Null. Weil es sich um einen Wendepunkt von F handelt, muss die zweite Ableitung von F gleich Null sein und nicht etwa die zweite Ableitung von f . (Die zweite Ableitung von F ist aber gleich der ersten Ableitung von f .) Daher muss gelten:
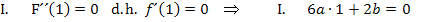


Die zweite Gleichung erhält man mit Hilfe der Information „ F hat ein Extremum bei x = 4“. Bei Extrempunkten verläuft die Tangente waagrecht und somit ist die Steigung/erste Ableitung dort gleich Null. Weil es sich um ein Extremum von F handelt, muss die erste Ableitung von F gleich Null sein und nicht etwa die erste Ableitung von f . (Die erste Ableitung von F ist aber gleich der Funktion f .) Es muss gelten:

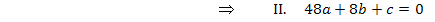
Die dritte Gleichung erhält man mit Hilfe der Information „F hat bei x = 0 die Steigung 3“. Es geht also um die Steigung/erste Ableitung von F und nicht um die Steigung/erste Ableitung von f . (Die erste Ableitung von F ist aber gleich der Funktion f .) Es muss gelten:
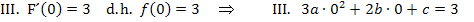

Jetzt setzen wir den ermittelten Wert für c in II. ein. Das ergibt:
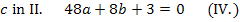
Nun liegen zwei Gleichungen mit den zwei Unbekannten a und b vor. Man nennt so etwas ein 2,2 – Gleichungssystem.


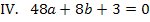
Das Gleichungssystem kann nun entweder mit dem Einsetzungsverfahren oder mit dem Additionsverfahren gelöst werden. Nimm einfach das Verfahren, das dir besser liegt. Im Folgenden findest du beide Methoden. Es reicht hier, wenn du eines kannst. (Für andere Rechnungen solltest du allerdings beide Lösungsverfahren für Gleichungssysteme beherrschen. Ausführliche Erklärungen bei Gleichungssysteme:Zwei Gleichungen für zwei Unbekannte und bei Gleichungssysteme:Drei Gleichungen für drei Unbekannte)
1. Methode:Einsetzungsverfahren
Eine der beiden Gleichungen wird nach einer der beiden Unbekannten aufgelöst und in die andere Gleichung eingesetzt. Hier bietet es sich an, die Gleichung I. nach b aufzulösen und nachher in II. einzusetzen. (Gleichung I. lässt sich nämlich gut nach b auflösen, weil dabei keine Brüche entstehen.

