Die Integralfunktion und der HDI

Weil es sich dann bei x = a um eine Nullstelle von F handelt, gilt für die y-Koordinate des Punktes:

y = F(a) = 0

Die y-Koordinate zu einer anderen x-Koordinate 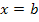kann nur durch Einsetzen von 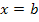in F berechnet werden. Das ist jedoch nur dann möglich, wenn man das Integral berechnen kann, d.h. wenn man eine Stammfunktion zu f finden kann. Ob man zuerst die integralfreie Form von 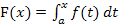berechnet und dann für x den entsprechenden Wert b einsetzt, oder ob man als erstes für die obere Grenze x den entsprechenden Wert b einsetzt und dann das bestimmte Integral 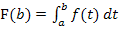berechnet, ist egal. Das Ergebnis ist die zugehörige y-Koordinate des Punktes von F mit der x-Koordinate 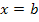. Lässt sich jedoch keine Stammfunktion zu f finden, ist es nicht möglich, die y-Koordinate dieses Kurvenpunktes von F zu ermittelt. In solchen Fällen ist daher nur nach der x-Koordinate gefragt.

Zu 4d.)

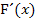Es soll die Gleichung der Wendetangente berechnet werden. Eine Wendetangente ist eine lineare Funktion und erfüllt daher die Gleichung . Als erstes muss ihre Steigung m berechnet werden. Die erste Ableitung einer Funktion entspricht bekanntlich ihrer Tangentensteigung. Da wir hier eine Wendetangente von F suchen und nicht von f, müssen wir die erste Ableitung und nicht 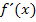verwenden. Um die Steigung m der Wendetangente von F zu berechnen, setzen wir die x-Koordinate des Wendepunktes 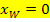in 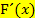, also in 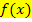ein. Laut HDI gilt ja 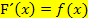. Den y-Achsenabschnitt t erhalten wir, wenn wir den vorab berechneten Wert der Steigung und die Koordinaten von W(0|0) in einsetzen und nach t auflösen.

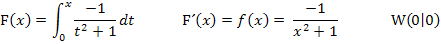
1. Steigung m berechnen:

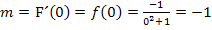
2. y-Achsenabschnitt t berechnen:

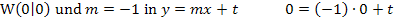
Die Gleichung der Wendetangente lautet: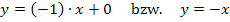

5. Bsp.:Funktionsgleichung einer Integralfunktion aufstellen

Eine Funktion lässt sich in der Form 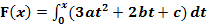schreiben.

Der Graph von F hat an der Stelle x = 1 einen Wendepunkt, an der Stelle x = 4 einen Extrempunkt und bei x = 0 eine Tangente mit der Steigung 3. Bestimme die Gleichung von F in integralfreier Darstellung!

Lösung:

Vorweg ermitteln wir die integralfreie Darstellung der Integralfunktion 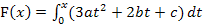, ohne für a, b und c etwas einzusetzen. Dann schreiben wir die erste und zweite Ableitung von F auf, auch wieder ohne für a, b und c etwas einzusetzen.

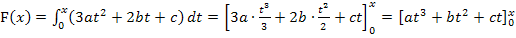
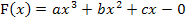
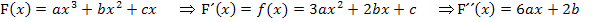
Hinweis:Man hätte die integralfreie Darstellung von F nicht unbedingt gleich zu Beginn ermitteln müssen. Die Aufgabe lässt sich natürlich auch mit Hilfe des HDI lösen, also mit dem Zusammenhang 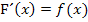und  entsprechend .

---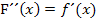