Die Integralfunktion und der HDI
Wir können also einfach den Zähler gleich Null setzen. (Wenn du mit dem Nenner multiplizierst, kommst du zum gleichen Ergebnis.)
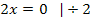
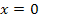
Für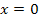 
gilt also 
. Außerdem wechselt 
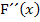bei 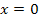das Vorzeichen, es liegt daher an der Stelle 
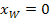ein Wendepunkt vor.
Dir ist nicht klar, warum sich das Vorzeichen von 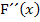bei 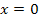ändert? Das ist hier ganz leicht zu erklären:Der Nenner von 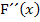, d.h. 
ist immer positiv, nur der Zähler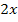 
kann entweder positiv oder negativ sein. Setzt man für x eine Zahl kleiner Null ein, ist der Ausdruck 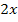negativ. Setzt man umgekehrt eine positive Zahl für x ein, so ist 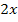positiv. Wegen Minus durch Plus ist Minus, ist 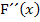für negative x ebenfalls negativ. Für positive x ist 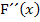positiv, weil Plus durch Plus wieder Plus ergibt. Weil sich an der Stelle 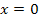das Vorzeichen von 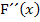ändert, ändert sich dort auch das Krümmungsverhalten von F und es liegt ein Wendepunkt von F vor.
Hier das Krümmungsverhalten von F in Tabellenform dargestellt:
 x |
 |
|
 |
 |
 |
 |
 |
 |
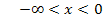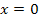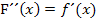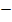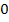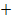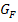rechts gekrümmt | WP | links gekrümmt |
Damit haben wir nachgewiesen, dass F genau einen Wendepunkt mit der Abszisse (d.h. x-Koordinate) 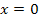hat. In dieser Aufgabe ist aber nicht nur nach der Abszisse des Wendepunkts gefragt, sondern nach beiden Koordinaten, also auch nach der y-Koordinate. (Oftmals ist bei Integralfunktionen nämlich ausschließlich nach der x-Koordinate, der sogenannten Abszisse, eines Extremums oder Wendepunktes gefragt. Dann musst du die y-Koordinate natürlich nicht berechnen. In der Regel ist die Berechnung der y-Koordinate für dich in solchen Aufgaben gar nicht möglich.) Wir müssen hier die y-Koordinate 
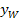des Wendepunktes von F allerdings schon noch ermitteln. Dazu könnten wir die x-Koordinate des Wendepunkts 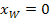in die Gleichung der Integralfunktion 
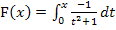einsetzen, weil es sich schließlich um einen Kurvenpunkt von F handelt. Wie du weißt, setzt man die x-Koordinate des Kurvenpunktes immer in diejenige Funktion ein, auf welcher der Punkt liegt. Wenn ein Punkt auf F liegt, muss man natürlich auch in die Funktionsgleichung von F einsetzen und nicht etwa in die Funktionsgleichung von f.
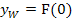
Hier kann man sich die Arbeit jedoch sparen, denn bei 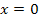liegt ja eine Nullstelle vor. Daher muss die y-Koordinate gleich Null sein. Somit gilt: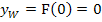 
Der Wendepunkt von F ist W(0|0).
Hinweis:Die y-Koordinate eines Kurvenpunkts einer Integralfunktion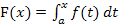 
kann man nur dann ohne Verwendung der integralfreien Form von F angeben, wenn die zugehörige x-Koordinate mit der unteren Grenze a von F übereinstimmt.
