Die Integralfunktion und der HDI
Die Funktion F aus unserer Aufgabe ist jedoch nachgewiesener Weise (vgl. Teilaufgabe 4a.) streng monoton fallend und in ihrer gesamten Definitionsmenge stetig. Also kann F die x-Achse nicht mehrmals schneiden. 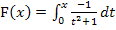 hat bei
hat bei 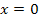 (untere Grenze) somit die einzige Nullstelle. Dadurch ist gezeigt, dass F genau eine Nullstelle hat. Diese liegt bei
(untere Grenze) somit die einzige Nullstelle. Dadurch ist gezeigt, dass F genau eine Nullstelle hat. Diese liegt bei 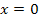 .
.
| Merke:
Ist eine Integralfunktion F einer stetigen Funktion f streng monoton, d.h. F ist nur steigend oder nur fallend, hat F genau eine Nullstelle. Eine Integralfunktion F ist genau dann streng monoton, wenn ihre Ableitung F´(x) immer positiv oder immer negativ ist. Laut HDI gilt Sollst du zeigen, dass eine Integralfunktion |
Zu 4c.)
Es soll gezeigt werden, dass 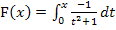 genau einen Wendepunkt besitzt. Außerdem sollen die Koordinaten des Wendepunktes angegeben werden.
genau einen Wendepunkt besitzt. Außerdem sollen die Koordinaten des Wendepunktes angegeben werden.
Überlege dir vorweg, wie du bei einer Funktion  die Wendepunkte berechnen würdest.
die Wendepunkte berechnen würdest.
Zur Erinnerung:Wendepunkte von f sind diejenigen Kurvenpunkte, wo sich das Krümmungsverhalten der Funktion f ändert. Man berechnet sie, indem man die Zweite Ableitung f ´´(x) gleich Null setzt. (Die zweite Ableitung von f entspricht dem Krümmungsverhalten von f.)
Um nun die Wendepunkte einer Integralfunktion F(x) zu berechnen, muss entsprechend die zweite Ableitung von F gleich Null gesetzt werden:
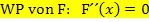
Laut HDI gilt 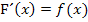 und somit auch
und somit auch 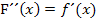 .
.
Um die zweite Ableitung von F zu bilden, müssen wir daher die erste Ableitung der Integrandenfunktion 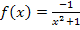 berechnen. Leite
berechnen. Leite  doch gleich ´mal alleine ab!
doch gleich ´mal alleine ab!
Du kannst das entweder mit der Quotientenregel oder auch nach Umformung mit dem Potenzgesetz 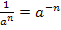 mit der Kettenregel machen. Wir wählen hier die Methode mit der Quotientenregel.
mit der Kettenregel machen. Wir wählen hier die Methode mit der Quotientenregel.
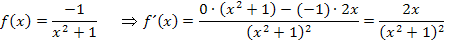
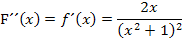
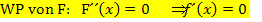
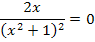
Ein Bruch ist gleich Null, wenn der Zähler gleich Null ist und der Nenner nicht gleich Null ist. Der Nenner kann hier nicht gleich Null werden, denn 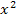 kann nicht negativ sein wegen der geraden Potenz.
kann nicht negativ sein wegen der geraden Potenz. 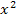 müsste aber gleich -1 sein, damit der Nenner Null ergibt.
müsste aber gleich -1 sein, damit der Nenner Null ergibt.

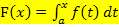
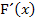 d.h.
d.h. 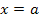 , wobei a für die untere Grenze der Integralfunktion steht.
, wobei a für die untere Grenze der Integralfunktion steht.