Streifenmethode für Integrale mit der allgemeinen unteren Grenze a
Streifenmethode für Integrale mit der allgemeinen unteren Grenze a
Will man ein bestimmtes Integral 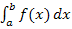 mit der allgemeinen unteren Grenze a berechnen, kann auch für
mit der allgemeinen unteren Grenze a berechnen, kann auch für 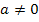 direkt die Streifenmethode verwendet werden.
direkt die Streifenmethode verwendet werden.
Bei Funktionen 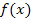 , die im Intervall von a bis b streng monoton steigend sind, gelten folgende allgemeine Ansätze für Ober- bzw. Untersumme.
, die im Intervall von a bis b streng monoton steigend sind, gelten folgende allgemeine Ansätze für Ober- bzw. Untersumme.
Obersumme: 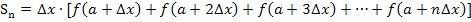
Untersumme:
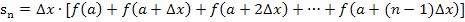
Bei Funktionen 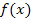 , die im Intervall von a bis b streng monoton fallend sind, gelten folgende allgemeine Ansätze für Ober- bzw. Untersumme.
, die im Intervall von a bis b streng monoton fallend sind, gelten folgende allgemeine Ansätze für Ober- bzw. Untersumme.
Obersumme: 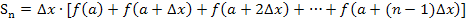
Untersumme:
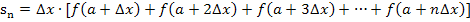
Bei streng monoton fallenden Funktionen 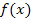 sind die Ansätze von Ober- und Untersumme genau vertauscht im Vergleich zu streng monoton steigenden Funktionen.
sind die Ansätze von Ober- und Untersumme genau vertauscht im Vergleich zu streng monoton steigenden Funktionen.
Wie man auf diese Ansätze kommt, werden wir nun besprechen. Wir behandeln zuerst den Fall, dass die Integrandenfunktion 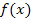 im Intervall von a bis b streng monoton steigend ist.
im Intervall von a bis b streng monoton steigend ist.
Mit der Streifenmethode zu berechnen: 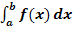
Voraussetzung:Integrandenfunktion 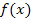 streng monoton steigend
streng monoton steigend
Anzahl der Streifen:n
Streifenbreite: 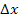
Berechnung der Obersumme 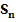 :
:
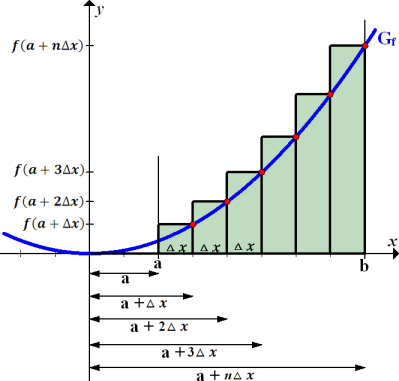
Abb. 14:Zur Berechnung der Obersumme 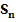 im Intervall a bis b
im Intervall a bis b
Hinweis:In Abb. 14 sind offensichtlich 6 Streifen dargestellt, doch musst du dir vorstellen, dass es sich allgemein um n Streifen handeln soll. Zu sehen ist in Abb. 14 also natürlich die Obersumme 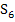 . Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete, natürliche Zahl für n zu wählen. n = 6 ist nur als beliebiges Beispiel anzusehen. Betrachte den letzten Streifen am besten als den n.ten Streifen und nicht einfach als den sechsten!
. Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete, natürliche Zahl für n zu wählen. n = 6 ist nur als beliebiges Beispiel anzusehen. Betrachte den letzten Streifen am besten als den n.ten Streifen und nicht einfach als den sechsten!
Alle n Streifen besitzen die gleiche Streifenbreite 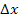 . Die Streifenhöhe ergibt sich jeweils aus der y-Koordinate des höchsten Kurvenpunktes innerhalb der einzelnen Streifen. (Bei der Obersumme wird schließlich die Oberkante des Streifens immer vom höchsten Kurvenpunkt des Streifens ausgehend gezeichnet.) Da der Graph streng monoton steigend ist, gehört zur höchsten y-Koordinate auch die höchste x-Koordinate im jeweiligen Streifen. Daher liegen die entsprechenden Punkte immer am rechten Rand des Streifens. (In Abb. 14 rot markierte Punkte) Diese Punkte liegen also immer in der rechten, oberen Ecke der einzelnen Streifen. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der entsprechenden x-Koordinaten in die Funktion
. Die Streifenhöhe ergibt sich jeweils aus der y-Koordinate des höchsten Kurvenpunktes innerhalb der einzelnen Streifen. (Bei der Obersumme wird schließlich die Oberkante des Streifens immer vom höchsten Kurvenpunkt des Streifens ausgehend gezeichnet.) Da der Graph streng monoton steigend ist, gehört zur höchsten y-Koordinate auch die höchste x-Koordinate im jeweiligen Streifen. Daher liegen die entsprechenden Punkte immer am rechten Rand des Streifens. (In Abb. 14 rot markierte Punkte) Diese Punkte liegen also immer in der rechten, oberen Ecke der einzelnen Streifen. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der entsprechenden x-Koordinaten in die Funktion 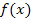 .
.
Nun stellt sich allerdings die Frage, welche x-Koordinaten diese Punkte besitzen. In Abb. 14 ist zu erkennen, dass der erste rot markierte Punkt (von links) die x-Koordinate 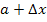 besitzt. Der zweite Punkt (von links) hat die x-Koordinate
besitzt. Der zweite Punkt (von links) hat die x-Koordinate 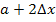 , der dritte Punkt
, der dritte Punkt 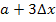 usw. bis zum n.ten und letzten Punkt, der die x-Koordinate
usw. bis zum n.ten und letzten Punkt, der die x-Koordinate 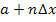 besitzt. Dabei gilt:
besitzt. Dabei gilt: 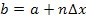
Der erste Streifen (von links) besitzt daher die Höhe 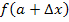 , der zweite Streifen entsprechend
, der zweite Streifen entsprechend 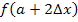 , der dritte Streifen
, der dritte Streifen 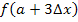 usw. bis zum n.ten und letzten Streifen, der dann die Höhe
usw. bis zum n.ten und letzten Streifen, der dann die Höhe 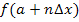 haben muss. Betrachte dazu noch einmal Abb.14!
haben muss. Betrachte dazu noch einmal Abb.14!
Nun berechnen wir die Obersumme 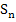 , indem wir bei jedem der n Streifen „Breite
, indem wir bei jedem der n Streifen „Breite 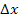 mal Höhe
mal Höhe 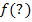 “ rechnen und alle Ergebnisse addieren.
“ rechnen und alle Ergebnisse addieren.
Beachte, dass sich zwar die x-Koordinaten ändern, die in 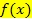 eingesetzt werden sollen, nicht aber die Streifenbreite
eingesetzt werden sollen, nicht aber die Streifenbreite 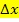 . Alle Streifen haben schließlich die gleiche Breite
. Alle Streifen haben schließlich die gleiche Breite 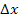 , nur die Höhe der Streifen hängt von der x-Koordinate des entsprechenden Kurvenpunkts ab.
, nur die Höhe der Streifen hängt von der x-Koordinate des entsprechenden Kurvenpunkts ab.
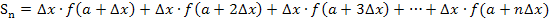
Wir klammern jetzt die Streifenbreite 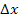 aus.
aus.
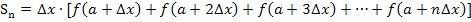
Als nächstes müssen wir 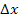 durch a, b und n ausdrücken, da wir die Obersumme ausschließlich in Abhängigkeit von a, b und n berechnen wollen. Der Ausdruck
durch a, b und n ausdrücken, da wir die Obersumme ausschließlich in Abhängigkeit von a, b und n berechnen wollen. Der Ausdruck 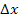 soll im Ergebnis nicht mehr vorkommen;nur noch a, b und n dürfen letztendlich enthalten sein. Wie kann man also
soll im Ergebnis nicht mehr vorkommen;nur noch a, b und n dürfen letztendlich enthalten sein. Wie kann man also 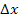 aus a, b und n berechnen? Da die Fläche (zwischen
aus a, b und n berechnen? Da die Fläche (zwischen 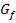 und der x-Achse) von a bis b gesucht ist, hat die gesamte Intervallbreite den Wert b - a. Die Strecke b - a wird in n gleich lange Stücke geteilt. Dann hat jedes einzelne Stück die Länge
und der x-Achse) von a bis b gesucht ist, hat die gesamte Intervallbreite den Wert b - a. Die Strecke b - a wird in n gleich lange Stücke geteilt. Dann hat jedes einzelne Stück die Länge 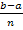 . Das entspricht exakt der Breite eines der Streifen.
. Das entspricht exakt der Breite eines der Streifen.
Daher gilt für die Streifenbreite 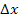 :
:
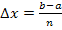
Damit ergibt sich allgemein für die Obersumme streng monoton steigender Funktionen 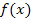 :
:
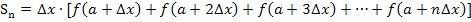
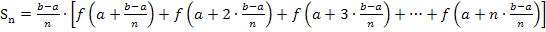
Danach muss mit der konkreten Funktionsgleichung von 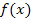 weiter gerechnet werden. Der weitere Rechenweg hängt also von der jeweiligen Funktion
weiter gerechnet werden. Der weitere Rechenweg hängt also von der jeweiligen Funktion 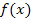 ab. Die Rechnung ist für
ab. Die Rechnung ist für 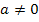 allerdings extrem aufwendig.
allerdings extrem aufwendig.
Nun zur Berechnung der Untersumme einer streng monoton steigenden Funktion 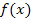 .
.
Berechnung der Untersumme 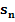 :
:
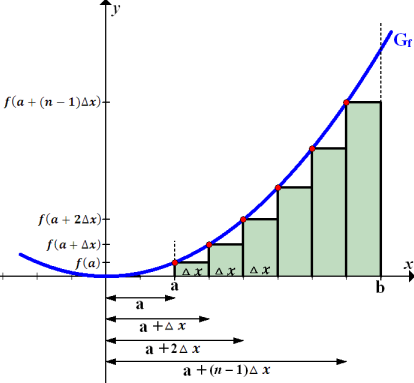
Abb. 15:Zur Berechnung der Untersumme 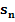 im Intervall a bis b
im Intervall a bis b
Hinweis:In Abb. 15 sind offensichtlich 6 Streifen dargestellt. Du musst dir allerdings vorstellen, dass es sich allgemein um n Streifen handeln soll. Zu sehen ist in Abb. 15 natürlich die Untersumme 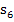 . Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete Zahl für n zu wählen. n = 6 ist also nur ein beliebiges Beispiel. Fasse den größten und letzten Streifen am besten als den n.ten Streifen auf und nicht einfach als den sechsten! Entsprechend ist der vorletzte Streifen nicht als der fünfte, sondern als der (n – 1).te Streifen zu verstehen.
. Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete Zahl für n zu wählen. n = 6 ist also nur ein beliebiges Beispiel. Fasse den größten und letzten Streifen am besten als den n.ten Streifen auf und nicht einfach als den sechsten! Entsprechend ist der vorletzte Streifen nicht als der fünfte, sondern als der (n – 1).te Streifen zu verstehen.
Alle n Streifen besitzen die gleiche Streifenbreite 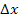 . Die Streifenhöhe ergibt sich jeweils aus der y-Koordinate des tiefsten Kurvenpunktes innerhalb der einzelnen Streifen. (Bei der Untersumme wird schließlich die Oberkante des Streifens immer vom tiefsten Kurvenpunkt des Streifens ausgehend gezeichnet.) Da der Graph streng monoton steigend ist, gehört zur niedrigsten y-Koordinate auch die niedrigste x-Koordinate im jeweiligen Streifen. Daher liegen die entsprechenden Punkte immer am linken Rand des Streifens. (In Abb. 15 rot markierte Punkte) Diese Punkte liegen also immer in der linken, oberen Ecke der einzelnen Streifen. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der entsprechenden x-Koordinaten in die Funktion
. Die Streifenhöhe ergibt sich jeweils aus der y-Koordinate des tiefsten Kurvenpunktes innerhalb der einzelnen Streifen. (Bei der Untersumme wird schließlich die Oberkante des Streifens immer vom tiefsten Kurvenpunkt des Streifens ausgehend gezeichnet.) Da der Graph streng monoton steigend ist, gehört zur niedrigsten y-Koordinate auch die niedrigste x-Koordinate im jeweiligen Streifen. Daher liegen die entsprechenden Punkte immer am linken Rand des Streifens. (In Abb. 15 rot markierte Punkte) Diese Punkte liegen also immer in der linken, oberen Ecke der einzelnen Streifen. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der entsprechenden x-Koordinaten in die Funktion 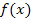 .
.
Nun stellt sich allerdings wieder die Frage nach den x-Koordinaten dieser Punkte. In Abb. 15 ist zu erkennen, dass der erste rot markierte Punkt (von links) die x-Koordinate 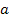 besitzt. Der zweite Punkt (von links) hat die x-Koordinate
besitzt. Der zweite Punkt (von links) hat die x-Koordinate 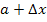 , der dritte Punkt
, der dritte Punkt 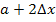 usw. bis zum n.ten und letzten Punkt, der die x-Koordinate
usw. bis zum n.ten und letzten Punkt, der die x-Koordinate 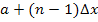 besitzt.
besitzt.
Der erste Streifen (von links) besitzt daher die Höhe 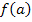 , der zweite Streifen entsprechend
, der zweite Streifen entsprechend 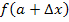 , der dritte Streifen
, der dritte Streifen 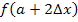 usw. bis zum n.ten und letzten Streifen, der dann die Höhe
usw. bis zum n.ten und letzten Streifen, der dann die Höhe 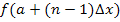 haben muss. Betrachte dazu noch einmal Abb.15!
haben muss. Betrachte dazu noch einmal Abb.15!
Nun berechnen wir die Untersumme 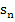 , indem wir bei jedem der n Streifen „Breite
, indem wir bei jedem der n Streifen „Breite 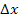 mal Höhe
mal Höhe 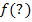 “ rechnen und alle Ergebnisse addieren.
“ rechnen und alle Ergebnisse addieren.
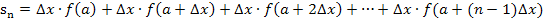
Wir klammern die Streifenbreite 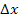 aus.
aus.
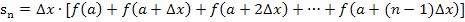
Mit 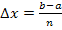 ergibt sich:
ergibt sich:
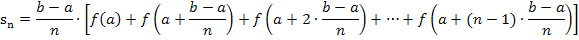
Danach muss mit der konkreten Funktionsgleichung von 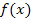 weiter gerechnet werden. Der weitere Rechenweg hängt also von der jeweiligen Funktion
weiter gerechnet werden. Der weitere Rechenweg hängt also von der jeweiligen Funktion 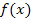 ab. Für
ab. Für 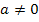 wird die Rechnung allerdings extrem aufwendig. Daher wird in der Schule in konkreten Aufgaben nur der Sonderfall a = 0 mit der allgemeinen Streifenanzahl n berechnet. Für
wird die Rechnung allerdings extrem aufwendig. Daher wird in der Schule in konkreten Aufgaben nur der Sonderfall a = 0 mit der allgemeinen Streifenanzahl n berechnet. Für 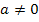 ist grundsätzlich eine konkrete Streifenanzahl angegeben;dann ist die Berechnung nicht mehr schwer, weil man richtige Zahlen hat, die man einsetzen kann.
ist grundsätzlich eine konkrete Streifenanzahl angegeben;dann ist die Berechnung nicht mehr schwer, weil man richtige Zahlen hat, die man einsetzen kann.
Ist die Integrandenfunktion 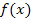 im Intervall von a bis b streng monoton fallend, sind die Ansätze für Obersumme und Untersumme im Vergleich zu einer steigenden Funktion
im Intervall von a bis b streng monoton fallend, sind die Ansätze für Obersumme und Untersumme im Vergleich zu einer steigenden Funktion 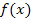 genau vertauscht. Woran liegt das?
genau vertauscht. Woran liegt das?
Bei streng monoton fallenden Funktionen besitzt der Punkt mit der höchsten y-Koordinate in einem bestimmten Streifen die jeweils niedrigste x-Koordinate dieses Streifens. Genau umgekehrt ist es bei streng monoton steigenden Funktionen:Dabei hat der Punkt mit der höchsten y-Koordinate in einem bestimmten Streifen auch die jeweils höchste x-Koordinate. Entsprechend gehört zu dem Punkt mit der jeweils niedrigsten y-Koordinate bei einer streng monoton fallenden Funktion die höchste x-Koordinate in diesem Streifen, während bei streng monoton steigenden Funktionen zum Punkt mit der niedrigsten y-Koordinate auch die niedrigste x-Koordinate gehört.
Deshalb liegen bei streng monoton steigenden Funktionen die für die Berechnung der Streifenhöhe benötigten Kurvenpunkte bei der Obersumme immer am rechten Rand der einzelnen Streifen und bei der Untersumme am linken Rand.
Bei streng monoton fallenden Funktionen ist es genau umgekehrt. Da liegen die Kurvenpunkte, deren y-Koordinaten die Streifenhöhen liefern, bei der Obersumme immer am linken Rand und bei der Untersumme am rechten Rand der Streifen.
Das kannst du auch an den nachfolgenden Abbildungen sehen.
|
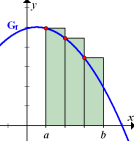
Abb.: Obersumme zu einer fallenden Funktion Die y-Koordinaten der rot markierten Kurvenpunkte liefern die Streifenhöhen. Sie liegen immer am linken Rand der Streifen.
|
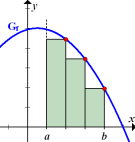
Abb.: Untersumme zu einer fallenden Funktion Die y-Koordinaten der rot markierten Kurvenpunkte liefern die Streifenhöhen. Sie liegen immer am rechten Rand der Streifen. |
|
Abb.: Obersumme zu einer steigenden Funktion Die y-Koordinaten der rot markierten Kurvenpunkte liefern die Streifenhöhen. Sie liegen immer am rechten Rand der Streifen.
|
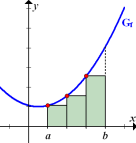
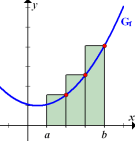
Abb.: Untersumme zu einer steigenden Funktion Die y-Koordinaten der rot markierten Kurvenpunkte liefern die Streifenhöhen. Sie liegen immer am linken Rand der Streifen. |
Zusammenfassung:
Bei streng monoton fallenden Funktionen:Der Punkt mit der höchsten y-Koordinate hat die niedrigste x-Koordinate. Die Kurvenpunkte, deren y-Koordinaten die Streifenhöhen ergeben, liegen bei der Obersumme immer am linken Rand und bei der Untersumme am rechten Rand der Streifen.
Bei streng monoton steigenden Funktionen:Der Punkt mit der höchsten y-Koordinate hat auch die höchste x-Koordinate. Die Kurvenpunkte, deren y-Koordinaten die Streifenhöhen ergeben, liegen bei der Obersumme immer am rechten Rand und bei der Untersumme am linken Rand der Streifen.
Das ist der Grund, warum die Ansätze für Obersumme und Untersumme bei streng monoton fallenden Funktionen genau umgekehrt sind wie bei Ober- und Untersumme streng monotonsteigender Funktionen. Der Ansatz, der bei einer steigenden Funktion die Obersumme ergibt, liefert die Untersumme einer fallenden Funktion. Entsprechend ergibt der Ansatz, der bei einer steigenden Funktion die Untersumme ergibt, die Obersumme einer fallenden Funktion. Näher wollen wir hier auf die Ansätze für Ober- bzw. Untersumme fallender Funktionen 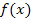 nicht eingehen.
nicht eingehen.