Allgemeine Hinweise zu der vorliegenden Funktion
Es handelt sich bei der Funktion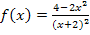 
um eine gebrochenrationale Funktion, da die Variable x im Nenner des Funktionsterms vorkommt. Für das Skizzieren des Graphen einer gebrochenrationalen Funktion ist besonders die Kenntnis der Asymptoten wichtig. Die Gleichungen der Asymptoten ergeben sich aus der Definitionslücke und dem Verhalten von 
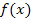im Unendlichen. (Dazu müsste man eigentlich die entsprechenden Grenzwerte berechnen;darauf verzichten wir an dieser Stelle bewusst. Man kann nämlich auch ohne weitere Rechnung nur durch den Funktionsterm viele Informationen über den Verlauf des Graphen gewinnen.)
Die Definitionslücke entspricht hier der senkrechten Asymptote von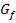 
. Sie liegt bei x = -2, weil für x = -2 der Nenner Null ergeben würde. Da die Klammer im Nenner nicht wegkürzbar ist, handelt es sich bei der Definitionslücke x = -2 um eine Polstelle, kurz Pol, und nicht um ein „Loch“ (genauer gesagt:stetig ergänzbare Definitionslücke, das sähe am Graph aus wie ein Loch.). Bei einer Polstelle hat der Graph immer eine senkrechte Asympote. Zu Erinnerung:Hätte sich die Klammer vollständig aus dem Nenner kürzen lassen, hätte ein „Loch“ vorgelegen.
Die Funktion hat also bei x = -2 eine Polstelle, d.h. eine senkrechte Asymptote. . Der Graph schmiegt sich von links und von rechts an die senkrechte Gerade x = -2 an. Es bleibt zu klären, ob es sich um einen Pol mit oder ohne Vorzeichenwechsel handelt. Es liegt hier ein Pol ohne Vorzeichenwechsel vor, d.h. der Graph schießt von beiden Seiten steil in dieselbe Richtung, also von links und rechts nach unten oder von beiden Seiten nach oben. (In diesem Fall nach unten;das kann man aber nicht direkt am Funktionsterm ablesen. Nur in der folgenden Abbildung sieht man es.) Dass es sich um einen Pol ohne Vorzeichenwechsel handelt, erkennt man am Funktionsterm 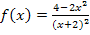an der Vielfachheit der Definitionslücke, also an der Potenz der Klammer im Nenner:Sie ist gerade;daher liegt ein Pol gerader Ordnung vor. Pole gerader Ordnung sind immer ohne Vorzeichenwechsel.
Die Gleichung der waagrechten Asymptote ergibt sich aus den Zahlen, die im Funktionsterm vor den höchsten x-Potenzen stehen. Dazu muss man sich die Klammer im Nenner ausgerechnet denken. (Zum Quadrieren der Klammer 1. Binomische Formel anwenden!)
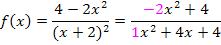
An dieser Form ist sofort zu erkennen, dass der Zählergrad gleich dem Nennergrad ist. (Zählergrad = höchste x-Potenz im Zähler;Nennergrad = höchste x-Potenz im Nenner) Wegen „Zählergrad gleich Nennergrad“ liegt überhaupt eine waagrechte Asymptote vor, deren Gleichung wir an den Zahlen vor den höchsten x-Potenzen erkennen können. Die Gleichung der waagrechten Asymptote lautet: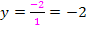 
Wir überlegen uns noch schnell die Schnittpunkte von 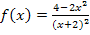mit den Achsen:
Schnittpunkt mit der y-Achse:
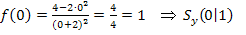
Schnittpunkte mit der x-Achse:
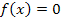
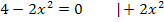
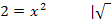
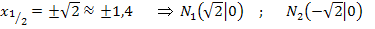
Mit diesen Ergebnisse können wir den Graph schon grob skizzieren. Für eine genauere Zeichnung ist eine Wertetabelle nötig.
Hier kannst du den Graph der Funktion 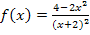sehen:
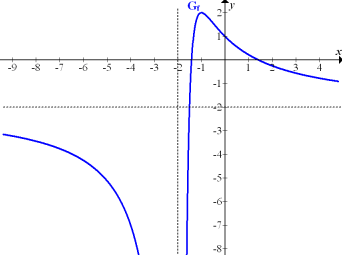
Abb.:Graph der gebrochenrationalen Funktion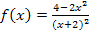 
mit seiner senkrechten Asymptote x = -2 und der waagrechten Asymptote y = -2
Ausführlichere Informationen dazu gibt es im gesonderten Kapitel:Kurvendiskussion gebrochenrationaler Funktionen
