Das Summenzeichen und die Streifenmethode
Dann muss man schließlich wissen, ob man nach x oder a bzw. t integrieren soll. Manchmal gibt es nämlich auch Aufgaben, wobei nach a oder nach t , also nach einer anderen Variablen als x integriert werden soll, dann steht da aber „da“ oder „dt“ und nicht „dx“ hinter dem Integral. Meist wird aber schon nach x integriert und deshalb steht fast immer „dx“ hinter dem Integral. Wenn x die Variable bezeichnet, musst du dx unbedingt hinter das Integral schreiben! Nicht vergessen! Nur so ist die Schreibweise des Integrals korrekt. Sobald man dann integriert hat, lässt man das „dx“ natürlich wieder weg. dx leitet sich von 
(sprich:„Delta x“) aus der Streifenmethode ab. Bei der Streifenmethode werden wir nachher die Streifenbreite mit bezeichnen. Dazu gleich noch mehr.
Merke:
Das bestimmte Integral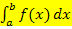 
entspricht dem Inhalt der Fläche A zwischen 
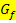und der x-Achse von a bis b, wenn die Fläche A oberhalb der x-Achse liegt und a <b gilt.
Wichtig:
Würde die Fläche A unterhalb der x-Achse liegen, wäre das Ergebnis des Integrals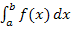 
negativ, zumindest wenn die untere Grenze a kleiner ist als die obere Grenze b. Man müsste dann den Betrag des Integrals verwenden, um wirklich den Flächeninhalt A zu erhalten. Das bestimmte Integral entspricht nämlich genau genommen der sogenannten Flächenbilanz. Dabei werden alle Flächenstücke zwischen 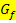und der x-Achse, die oberhalb der x-Achse liegen, positiv gezählt und alle unterhalb der x-Achse liegenden Flächenstücke negativ gezählt. Dies gilt aber nur, wenn für die Grenzen gilt:a <b
Vertauscht man die obere und untere Integrationsgrenze, dreht sich das Vorzeichen des Integrals um.
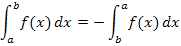
Das Integral ist daher für a >b, also bei „falscher Integrationsrichtung“ negativ, wenn die Fläche zwischen Graph 
und der x-Achse von a bis b oberhalb der x-Achse liegt, und entsprechend positiv, wenn die Fläche unterhalb der x-Achse liegt. (Mehr dazu auch im Teil:Anwendungen der Integralrechnung) Das bestimmte Integral 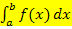ist also nicht immer genau das gleiche wie die Fläche zwischen Graph 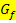und der x-Achse von a bis b! Die nächste Beispielaufgabe soll dazu dienen, dir den kleinen aber entscheidenden Unterschied zwischen bestimmten Integral und Fläche klar zu machen.
1. Bsp.:Der kleine, aber feine Unterschied zwischen Integral und Fläche
In der nachfolgenden Abbildung ist der Graph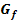 
einer Funktion 
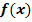sowie ein rosafarbenes Flächenstück 
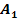und ein grünes Flächenstück 
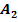zu sehen.
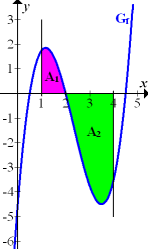
Das rosafarbene Flächenstück 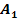hat einen Flächeninhalt von 1,3 FE. Das grüne Flächenstück 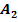besitzt einen Flächeninhalt von 6,2 FE. (FE steht dabei für „Flächeneinheiten“). Gib die Ergebnisse der folgenden Integrale und den gesamten Flächeninhalt 
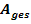der farbig markierten Fläche an!
