Das Summenzeichen und die Streifenmethode
Da jedoch in den meisten Schulbüchern in diesem Zusammenhang i verwendet wird, benützen wir auf dieser website ebenfalls durchgängig den Buchstaben i im Zusammenhang mit Potenzsummen und Reihen allgemein.)
Auf der Merkhilfe für Gymnasiasten des G8 sind die Formeln für Potenzsummen nicht enthalten. Aber keine Sorge, in Prüfungen kommt die Streifenmethode sowieso nicht dran und nur dafür brauchst du die Formeln der Potenzsummen. D.h. du musst die Formeln der Potenzsummen vor Prüfungen nicht auswendig lernen.
3. Bsp.:Berechne die Summe der ersten 20 Quadratzahlen unter Verwendung der entsprechenden Summenformel!
Lösung:
Die Summe der ersten 20 Quadratzahlen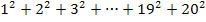 
kann mit Hilfe der Formel 
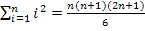schnell berechnet werden. Es gilt:n = 20
Wir müssen also nur für n die Zahl 20 in die Formel einsetzen und das Ergebnis davon berechnen.
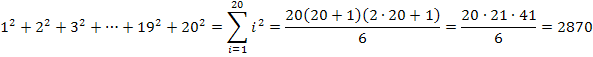
Nun aber endlich zum Integral und zur Streifenmethode selbst.
Wofür braucht man die Streifenmethode?
Mit Hilfe der Streifenmethode können sogenannte bestimmte Integrale näherungsweise berechnet und Formeln für deren exakte Berechnung hergeleitet werden. Doch was sind überhaupt bestimmte Integrale? Das müssen wir vorher erst noch genau klären.
Einführung des bestimmten Integrals
Gegeben ist die Gleichung einer stetigen Funktion 
. (Eine Funktion ist stetig, wenn ihr Graph keine Sprungstellen hat. Die Funktion soll also keine Sprungstellen haben.) Gesucht ist die Fläche A zwischen dem Graph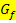 
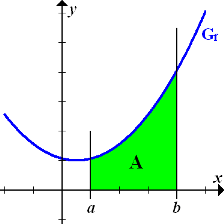
der gegebenen Funktion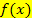 
und der x-Achse von der senkrechten Geraden x = a bis zur Geraden x = b. Dabei stellen a und b konkrete, feste Zahlen dar. Wir bezeichnen sie als untere bzw. obere Grenze. Es soll a <b gelten. a ist also die untere Grenze (linker Rand der Fläche);entsprechend ist b die obere Grenze (rechter Rand der Fläche). Vergleiche nachfolgende Abbildung! Sowohl a als auch b sind zusätzlich zur Funktionsgleichung von angegeben.
 |
|
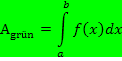
Wir führen ein neues mathematisches Zeichen ein:
Das bestimmte Integral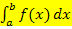 
(Sprich:„Integral von a bis b von f(x) dx“)
Die Funktion wird in diesem Zusammenhang als „Integrand“ oder „Integrandenfunktion“ bezeichnet.
Du fragst dich vielleicht, was das „dx“ hinter dem Integral bedeutet. Eigentlich ist „dx“ nur eine Schreibweise, die dir sagt, dass nach x integriert werden soll. Anders gesagt, das „dx“ verrät dir, dass hier x die Variable ist. Das ist so ähnlich wie bei , da steht auch in der Klammer immer die Variable x. Das „dx“ wird vor allem dann wichtig, wenn mehrere Buchstaben im Funktionsterm auftauchen, beispielsweise x und a oder t.
