Das Summenzeichen und die Streifenmethode
In unserem Beispiel sind die ersten 100 natürlichen Zahlen addiert worden, d.h. n = 100. Wir wollen nun eine Formel für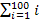 
entwickeln, in der die obere Grenze 100 vorkommt, um davon eine Formel für 
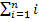herzuleiten.
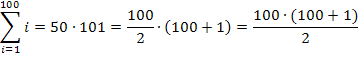
Nun ersetzen wir die konkrete obere Grenze 100 durch den Buchstaben n. So erhalten wir eine Formel für die Summe der natürlichen Zahlen von 1 bis n.
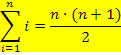
Wer sich nun fragt, was denn bei ungeradem n ist, beispielsweise bei n = 99, dem sei gesagt, dass die Formel immer stimmt, egal ob n gerade oder ungerade ist. Auf den Beweis oder eine Herleitung für ungerade Werte von n wird hier verzichtet. Es würde zu weit führen. Du kannst die Richtigkeit der Formel aber wenigstens für kleinere ungerade Werte von n einfach testen, indem du einmal die Summe mit Hilfe der Formel und ein zweites Mal durch bloßes Addieren der Zahlen berechnest. Wähle dazu beispielsweise n = 9. Du wirst feststellen, dass die Formel das richtige Ergebnis liefert, obwohl die Zahl 5 praktisch keinen Partner hat zum Addieren. Die 5 bleibt quasi übrig, weil in Gedanken jeweils die Zahlen 1 und 9 addiert werden, die 2 und die 8, die 3 und die 7, sowie die 4 und die 6.
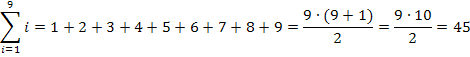
Die Zahl 5 hat also keinen Partner zum Addieren. Die Formel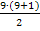 
stimmt dennoch. Das liegt daran, dass man sich die Zahl 5 auch als die Hälfte von 10 und somit als die Hälfte von 4,5 + 5,5 denken kann: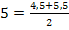 
Zur Kontrolle kannst du einfach die Zahlen 1 und 9, die Zahlen 2 und 8, die Zahlen 3 und 7, sowie die Zahlen 4 und 6 zu vier Pärchen mit der Summe 10 zusammenfassen und die übrig gebliebene Zahl 5 noch zu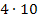 
dazu zählen.
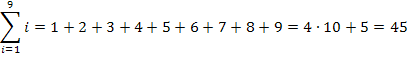
Du siehst, es kommt wieder das gleiche Ergebnis heraus. Die Formel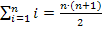 
stimmt also auch für n = 9, obwohl dies ein ungerades n ist. (Den allgemeinen mathematischen Beweis für n 
ℕ könnte man durch Induktion führen. Das Beweisverfahren Beweis durch Induktion steht nicht auf dem Lehrplan für Gymnasien in Bayern.)
Entsprechende Formeln gibt es auch für die Summe der Quadratzahlen von 1 bis n und für die Summe der dritten und vierten Potenzen. Auf die Herleitung der folgenden Formeln wird hier verzichtet. Du brauchst die Herleitungen sowieso nicht. Die Formeln werden wir aber nachher bei der Streifenmethode verwenden.
Weitere wichtige Formeln für Potenzsummen:
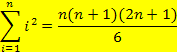
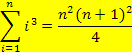
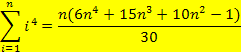
Schüler der FOS oder BOS finden diese Formeln auch in der bsv-Formelsammlung S. 51. (Statt dem Buchstaben i steht in der Formelsammlung allerdings der griechische Buchstabe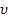 
.
