Das Summenzeichen und die Streifenmethode
Wir betrachten wie schon in Teilaufgabe 2d.) vorerst nur die einzelnen Zahlen ohne ihr Vorzeichen. Der Zähler der Brüche ist immer 1, der Nenner wird gebildet durch Potenzen der Zahl 5. Das erste Glied ist die Zahl 1, die ganz vorne steht;wir denken sie uns ebenfalls als Bruch mit dem Zähler 1 und einer Potenz von 5 im Nenner. Welche Potenz müssen wir da verwenden?
Richtig, wir brauchen beim ersten Glied die Potenz 0, wegen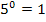 
gilt: 
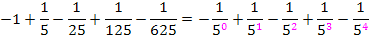
Zum ersten Glied gehört somit i = 0 und zum letzten Glied i = 4. Wären alle Vorzeichen positiv, würde man die Summe von 0 bis 4 von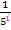 
bilden. Leider stehen vor den Gliedern mit geradem i negative Vorzeichen und nur bei den Gliedern mit ungeradem i positive Vorzeichen. Die entsprechenden Vorzeichen liefert die Multiplikation mit dem Ausdruck 
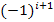. (Stattdessen könntest du z. B. auch 
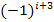oder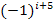 
verwenden. Da gibt es viele Möglichkeiten. Als Basis muss -1 verwendet werden;im Exponenten muss i plus eine beliebige ungerade Zahl stehen.)
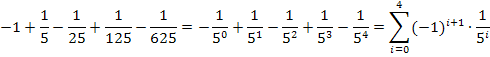
Zu 2f.)
Es soll die Summe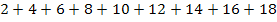 
mit dem Summenzeichen geschrieben werden. Es ist dir bestimmt aufgefallen, dass es sich hierbei um die Summe aller geraden Zahlen von 2 bis 18 handelt. Eine gerade Zahl ist laut Definition immer durch 2 teilbar und lässt sich daher als Vielfaches der Zahl 2 auffassen. Der Term 2i liefert ausschließlich gerade Zahlen, solange i eine natürliche Zahl darstellt und das ist bei einer Reihe schließlich der Fall.
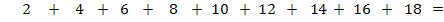
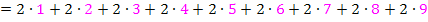
Das i durchläuft alle natürlichen Zahlen von 1 bis 9. Deshalb gilt:
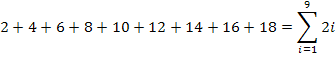
Zu 2g.)
Gesucht ist die Summenschreibweise von: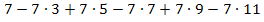 
Lassen wir zuerst die Vorzeichen außer Acht. Offensichtlich haben alle Glieder die Form „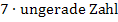 
“. Eine ungerade Zahl erhält man sicher, wenn man zu einer geraden Zahl 1 dazuzählt. Eine gerade Zahl ergibt sich durch 2i, entsprechend ergibt sich durch 2i + 1 immer eine ungerade Zahl. (Natürlich liefert auch 2i + 3 oder 2i + 5 eine ungerade Zahl. Aber am einfachsten ist eben 2i + 1.) Der Term 2i + 1 liefert für i = 0 die Zahl 1 und für i = 5 die Zahl 11. i muss hier demnach alle natürlichen Zahlen von 0 bis 5 durchlaufen.
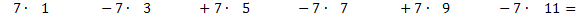
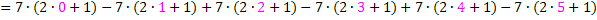
Wären alle Vorzeichen positiv, könnte man die Summe von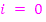 
bis 
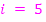von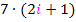 
bilden.
Wir müssen uns aber noch um die Vorzeichen kümmern. Bei Gliedern mit geradem i steht jeweils ein Plus, bei Gliedern mit ungeradem i steht ein Minus. Die entsprechenden Vorzeichen ergeben sich durch Multiplikation mit dem Ausdruck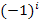 
.
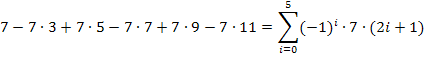
Alternativlösung:
Auch der Term 2i – 1 liefert ungerade Zahlen.
