Das Summenzeichen und die Streifenmethode

Wichtig:Beim Integrieren nach x werden multiplikative Konstanten einfach abgeschrieben, wogegen bei additiven Konstanten ein x dazu kommt. Einfacher gesagt:Zahlen, die multipliziert oder durch die dividiert wird, müssen beim Integrieren abgeschrieben werden. Zahlen ohne x mit Plus oder Minus erhalten dagegen ein x dazu. Sollst du zum Beispiel -9 nach x integrieren, muss du dich fragen, welche Funktion abgeleitet -9 ergibt. Das ist natürlich die Funktion -9x. Deshalb kommt beim Integrieren einer Zahl ohne x, die addiert oder subtrahiert wird, immer ein x dazu.

Schauen wir uns das Ganze an einem der Beispiele an, welche wir oben bereits mit den einzelnen Formeln aus der Streifenmethode berechnet haben.

Bsp.: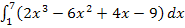

Zuerst ermitteln wir eine Stammfunktion. Sie wird in eckige Kammern und die Grenzen oben bzw. unten an die rechte Klammer geschrieben.

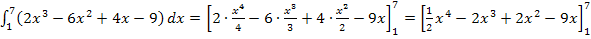
Als nächstes werden die Grenzen in die Stammfunktion eingesetzt:Obere minus untere! Vorsicht beim Einsetzen der unteren Grenze:Am besten eine Klammer darum setzen! Es muss schließlich der gesamte Term subtrahiert werden, der durch das Einsetzen der unteren Grenze entsteht. Stattdessen kannst du natürlich auch alle Vorzeichen umdrehen. Doch zu empfehlen ist eher die Klammer!

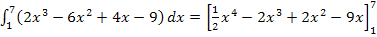
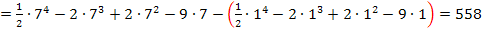
Offensichtlich kommt das gleiche Ergebnis heraus, wie bei der Rechnung weiter oben, wobei die einzelnen mit der Streifenmethode hergeleiteten Formeln verwendet wurden.

Der neue Weg, bestimmte Integrale mit Hilfe der Stammfunktion zu lösen, ist aber langfristig sicherlich der einfachere. Die Streifenmethode ist im Vergleich dazu sehr viel aufwendiger und arbeitsintensiver. Du wirst sie daher zukünftig nicht mehr brauchen. Nur die Schreibweise des Integrals mit dem „dx“ hinter dem Integranden erinnert dann noch an die ursprüngliche Herleitung mit der Streifenmethode. Das „dx“ leitet sich wohl von der immer kleiner werdenden Streifenbreite (sprich:„Delta x“) der einzelnen Streifen bei der Streifenmethode ab.

Wie man bei verschiedenen einfacheren Funktionen eine Stammfunktion ermittelt, wird ausführlicher im Teil Die Stammfunktion F(x) und einfache Integrationsregelnbehandelt. Wie du auch bei schwierigeren Funktionen eine Stammfunktion finden kannst, wird erklärt im Teil Weitere Integrationsregeln. Viele Beispielaufgaben zum Thema Integrale findest du außerdem im Teil Das bestimmte und das unbestimmte Integral. Wozu man Integrale generell brauchen kann, wird besprochen bei Anwendungen der Integralrechnung.

---