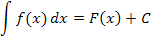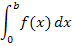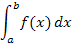Das Summenzeichen und die Streifenmethode

So ist 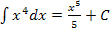nur eine andere Schreibweise für 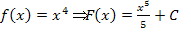. In anderen Worten:Direkt hinter dem Integralzeichen steht immer die zu integrierende Funktion und hinter dem Gleichheitszeichen stehen die Stammfunktionen F(x). Die Funktion wird in diesem Zusammenhang wie auch beim bestimmten Integral als „Integrand“ oder „Integrandenfunktion“ bezeichnet.

Bei 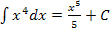ist beispielsweise 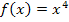der Integrand bzw. die Integrandenfunktion und das Ergebnis des unbestimmten Integrals 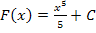die Menge aller zugehörigen Stammfunktionen.

Dir ist bestimmt längst die Ähnlichkeit der unbestimmten Integrale / Stammfunktionen zu den Formeln für die bestimmten Integrale (vor allem mit der unteren Grenze 0) aufgefallen, die wir vorher mit der Streifenmethode hergeleitet haben. Vergleiche:

Unbestimmtes Integral (Stammfunktion)	Bestimmtes Integral mit unterer Grenze 0 (mit Streifenmethode hergeleitet)	Bestimmtes Integral mit allgemeiner unterer Grenze a (mit Streifenmethode hergeleitet)

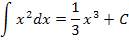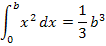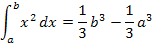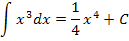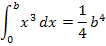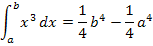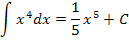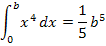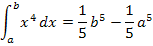Um ein bestimmtes Integral zu berechnen, bildet man zuerst eine Stammfunktion und setzt dann zuerst die obere Grenze b für x in die Stammfunktion ein. Danach setzt man die untere Grenze a ein und subtrahiert das Ergebnis. (Diese Vorgehensweise führt letztendlich bei 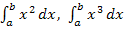und 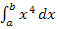ebenfalls zu den Formeln, die wir schon mit der Streifenmethode hergeleitet haben.) Mathematisch geschrieben sieht das Ganze so aus:

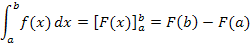
Wir berechnen das folgende Integral nach der neuen Methode: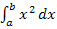

Dazu ermitteln wir zuerst eine Stammfunktion F(x) zu 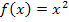. Das „ + C “ können wir beim bestimmten Integral weglassen;es würde nachher beim Einsetzen der Grenzen sowieso wieder herausfallen. Die Stammfunktion F(x) schreiben wir in eckige Klammern, wobei die Grenzen oben bzw. unten an die rechte Klammer geschrieben werden. (Die Stammfunktion erhalten wir, indem wir zum Exponenten von f die Zahl 1 dazuzählen und durch den neuen Exponenten dividieren.)

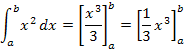
In einem zweiten Schritt werden die Grenzen in die Stammfunktion eingesetzt:Zuerst die Obere, dann minus die Untere!

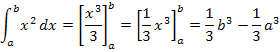
Du siehst, dass genau das gleiche Ergebnis heraus kommt wie bei der Streifenmethode. In Zukunft musst du also nicht erst mühselig mit der Streifenmethode arbeiten, wenn du das bestimmte Integral einer neuen Funktion berechnen sollst. Du musst nur eine Stammfunktion zu dieser Funktion ermitteln und dann die Grenzen einsetzen. Das ist doch wesentlich bequemer als die komplette Streifenmethode. Das einzige Problem daran ist, dass sich nicht immer so leicht eine Stammfunktion finden lässt. Integrieren ist bei komplizierteren Funktionen nämlich deutlich schwieriger als Ableiten.

---