Das Summenzeichen und die Streifenmethode

2. Bsp.:

Schreibe die folgenden Terme unter Verwendung des Summenzeichens!

a.)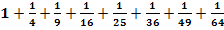

b.)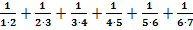

c.)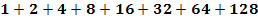

d.)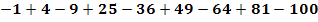

e.)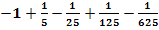

f.)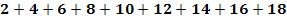

g.)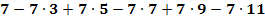

Lösung:

Zu 2a.)

Der Term 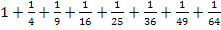soll in der Summenschreibweise geschrieben werden.

Kleiner Tipp:Denke dir die Zahl 1 als Bruch in der Form .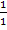

Was fällt dir am Nenner der einzelnen Summanden bei 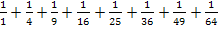auf? Richtig, es sind alles Quadratzahlen! Wir können also schreiben:

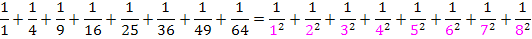
Die Summanden besitzen somit immer die Form 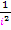, wobei i alle natürlichen Zahlen von 1 bis 8 durchlaufen soll. Deshalb kann man schreiben:

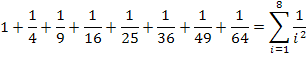
Zu 2b.)

Der Term 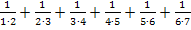soll mit Hilfe des Summenzeichens geschrieben werden. Dafür gibt es mehrere Möglichkeiten. Auf die erste Möglichkeit kommt man vermutlich am leichtesten. Im Nenner steht immer das Produkt zweier Zahlen, wobei die hintere Zahl immer um 1 größer ist als die vordere Zahl. Betrachtet man die vordere Zahl im Nenner als i , so ist die zweite entsprechend um 1 höher, also i + 1.

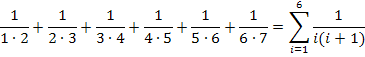
Aber auch die nächste Schreibweise ist korrekt.

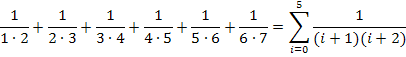
Es gibt noch viele weitere Möglichkeiten, den Term mit einem Summenzeichen zu schreiben. Doch sollen uns an dieser Stelle die oben gezeigten Varianten reichen.

Zu 2c.)

Der Term 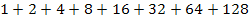soll mit dem Summenzeichen geschrieben werden.

Tipp:Denk daran, dass eine beliebige Zahl hoch Null genommen grundsätzlich 1 ergibt: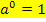

Überlege dir nun, was die Zahlen der einzelnen Summanden gemeinsam haben.

Du bist hoffentlich selbst darauf gekommen, dass es sich bei den Zahlen 1, 2, 4, 8, 16, 32, 64 und 128 allesamt um Potenzen der Zahl 2 handelt.

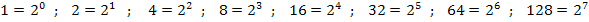
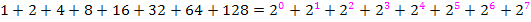
Es handelt sich also um die Summe der Zweierpotenzen 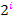mit den Exponenten i von 0 bis 7.

Zu 2d.)

Es soll die Summenschreibweise des Terms 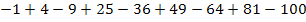gefunden werden.

Lassen wir vorerst die Vorzeichen außer Acht und betrachten nur die Zahlen ohne Vorzeichen. Da fällt dir bestimmt gleich auf, dass es sich ausschließlich um Quadratzahlen handelt. Die Zahlen 1, 4, 9, 16, 25, 36, 49, 64, 81 und 100 sind die Quadrate der Zahlen von 1 bis 10. Wären die Vorzeichen alle positiv, müssten wir die Summe der Quadratzahlen 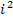von i = 1 bis 10 bilden. Doch leider steht bei allen ungeraden i ein negatives Vorzeichen und nur bei den geraden i ein Pluszeichen. Daher benötigen wir zusätzlich zu 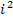den Ausdruck 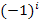. Dieser Ausdruck sorgt für den entsprechenden Vorzeichenwechsel;bei ungeradem i Minus und bei geradem i Plus.

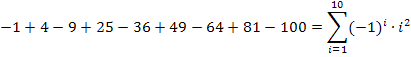
Zu 2e.)

Gesucht ist die Summenschreibweise von .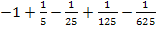

---