Das Summenzeichen und die Streifenmethode
Von der Streifenmethode zur Stammfunktion F(x) und zum allgemeinen Integralbegriff
Wozu eigentlich der ganze Aufwand mit der Streifenmethode? Geht es nicht auch einfacher? Erfreulicherweise lassen sich bestimmte Integrale auch folgendermaßen berechnen:
- Stammfunktion F(x) zur Funktion
ermitteln - Grenzen für x in die Stammfunktion einsetzen:Zuerst die obere Grenze, dann minus die Untere!
Doch was ist denn überhaupt eine Stammfunktion F(x) zu einer Funktion ? In der 11. Klasse habt ihr das bestimmt im Unterricht schon einmal kurz besprochen. Das ist aber schon einige Zeit her und vielleicht erinnerst du dich nicht mehr so genau daran. Daher noch einmal zur Wiederholung:
Wenn F(x) eine Stammfunktion zu einer Funktion ist, gilt laut Definition:
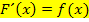
Will man eine Stammfunktion F(x) zu einer Funktion finden, muss man praktisch das Gegenteil vom Ableiten machen, also „hochleiten“ oder „aufleiten“. Die Begriffe „hochleiten“ oder „aufleiten“ sind in der Mathematik jedoch nicht gebräuchlich, korrekt heißt es „integrieren“.
Wie findet man eine Stammfunktion bzw. wie integriert man eine Funktion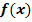 
?
Um zu einer Funktion der Form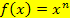 
eine Stammfunktion F(x) zu bilden, zählt man zum Exponenten die Zahl 1 dazu und teilt außerdem durch den neuen Exponenten. Dahinter schreibt man „ + C “. (Warum wird gleich noch erklärt.)
Bsp.:
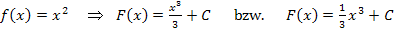
Hinweis:Ob du lieb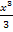er 
oder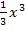 
schreibst, kannst du selbst entscheiden. Beide Schreibweisen sind im Prinzip gleich. Es gilt nämlich: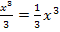 
Entsprechend gilt: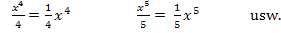 
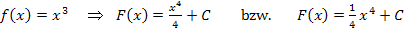
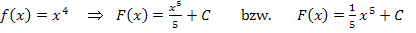
Allgemein:
Dabei steht C für eine beliebige reelle Konstante, also für irgendeine feste Zahl. Da eine Zahl + C beim Ableiten wegfällt, kann man sie umgekehrt beim Integrieren nicht konkret ermitteln. Daher schreibt man beim Integrieren einfach „+ C “ dahinter. Es gibt somit viele verschiedene Stammfunktionen F(x) zu einer Funktion , die sich nur in der additiven Konstante C unterscheiden. („Additive Konstante“ bedeutet „Zahl ohne x, die dazugezählt oder abgezogen wird.) Die Graphen der Stammfunktionen F(x) einer bestimmten Funktion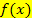 
gehen alle durch Verschiebung entlang der y-Achse nach oben oder unten auseinander hervor.
Wir führen jetzt eine neue Schreibweise ein.
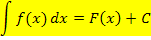
Vorher haben wir ausschließlich Integrale mit Grenzen gehabt, die sogenannten „bestimmten Integrale“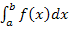 
. Das neue Integral 
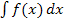hat aber keine Grenzen, daher wird es als „unbestimmtes Integral“ bezeichnet. Das unbestimmte Integral entspricht der Menge aller Stammfunktionen F(x) einer Funktion .
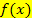