Das Summenzeichen und die Streifenmethode
Wenn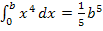 
gilt, muss entsprechend auch 
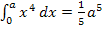gelten. Das Integral 
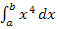entspricht der Fläche zwischen 
und der x-Achse von a bis b. Es kann berechnet werden, indem man die Fläche zwischen und der x-Achse von 0 bis b nimmt und davon die Fläche zwischen und der x-Achse von 0 bis a abzieht. Daher gilt:
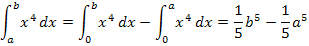
Damit haben wir auch die Formel für 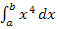hergeleitet:
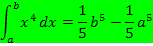
Nun haben wir alle zu Beginn erwähnten Grundintegrale mit Hilfe der Streifenmethode hergeleitet. Wir fassen noch einmal alle bisher hergeleiteten Formeln zusammen:
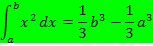
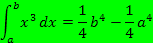
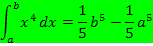
Des Weiteren gilt:
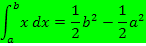
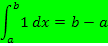
Auf die Herleitungen der letzten beiden Formeln verzichten wir hier. Diese beiden Formeln würden sich auch ohne Verwendung der Streifenmethode zeigen lassen, da die Funktionen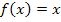 
und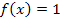 
keine Kurven, sondern Geraden sind.
Mit Hilfe der Streifenmethode lässt sich für beliebige konstante Zahlen c 
ℝ auch zeigen, dass gilt:
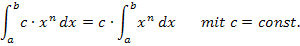
Allgemein:
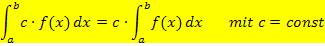
Diese Regel wird auch als „Faktorregel“ bezeichnet. Sie besagt im Prinzip nichts anderes als, dass man Konstanten, d.h. feste Zahlen ohne x, vor das Integral ziehen darf. Den Beweis ersparen wir uns hier bewusst;du brauchst ihn sowieso nicht.
Bsp.:
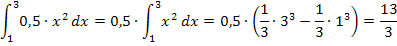
Außerdem kann gezeigt werden, dass die sogenannte „Additionsregel“ gilt. Sie lautet:
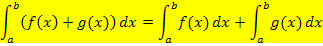
Diese Regel kann nicht nur auf Summen, sondern auch auf Differenzen von Funktionen angewendet werden. Im Prinzip besagt sie, dass man bei Summen bzw. Differenzen von mehreren Funktionen jede Funktion einzeln integrieren darf. Bei + oder – darf man also einzeln nacheinander integrieren. (Aber Vorsicht:Bei Produkten oder Quotienten darf man nicht einfach Faktor für Faktor einzeln integrieren bzw. Zähler und Nenner einzeln integrieren. Ein Produkt bzw. Quotient muss vor dem Integrieren zu einer Summe bzw. Differenz umgeformt werden. Produkte und Quotienten vor dem Integrieren falls möglich erst ausrechnen! Mehr dazu im Teil:Das bestimmte und das unbestimmte Integral)
Bsp.:
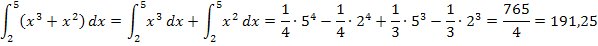
Die „Faktorregel“ kann auch mit der „Additionsregel“ kombiniert angewendet werden. Damit lassen sich bestimmte Integrale von allen ganzrationalen Funktionen / Polynomfunktionen berechnen.
Bsp.:
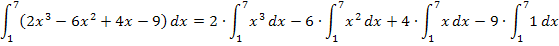
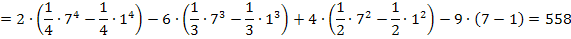
Das Prinzip ist an sich nicht schwierig, verlangt aber doch ungeheure Konzentration, dass man nicht durcheinander kommt. Bald wirst du aber eine andere Methode kennenlernen, wie du bestimmte Integrale mit Hilfe der Stammfunktion F(x) ausrechnen kannst. Der neue Weg ist deutlich angenehmer. Auch auf die Gefahr hin deinem Lehrer in der Schule schon etwas vorzugreifen, schauen wir uns gleich den neuen Weg kurz an, wie man bestimmte Integrale ausrechnen kann. Du wirst sehen, dass von den oben hergeleiteten Formeln nicht mehr weit zum neuen Weg ist.
