Das Summenzeichen und die Streifenmethode

h. sie werden für sehr große Werte von n vernachlässigbar klein.

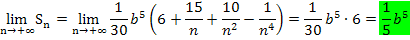
Berechnung der Untersumme :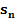

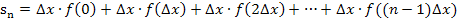
Wir klammern aus:

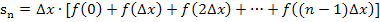
Mit 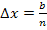ergibt sich:

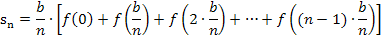
Damit du nachher leichter auf eine Gesetzmäßigkeit kommst, mit der du ein Summenzeichen einführen kannst, schreiben wir statt 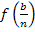 ab sofort: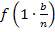

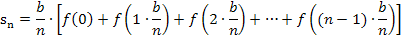
Dieser Ansatz für die Untersumme ist noch allgemein gültig für alle streng monoton steigenden Funktionen. Als nächstes setzen wir aber die x-Koordinaten 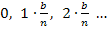bis 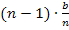in unsere gegebene Funktionsgleichung 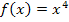ein, um 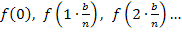bis 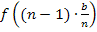zu ermitteln. Ab hier gilt die Rechnung nur speziell für .

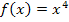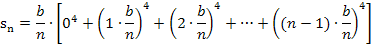
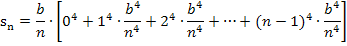
Zur Vereinfachung klammern wir wieder den Faktor 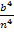aus. Das ergibt:

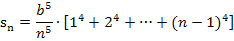
Den Ausdruck in der eckigen Klammer können wir mit dem Summenzeichen schreiben. In der Klammer steht die Summe der vierten Potenzen aller natürlichen Zahlen von 1 bis n – 1. Jetzt verwenden wir wieder die Formel für die Summe der dritten Potenzen.

Noch einmal zur Erinnerung:

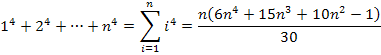
Leider stehen wir nun vor dem Problem, dass diese Formel eigentlich für die Summe der vierten Potenzen von 1 bis n gilt, wir hier allerdings die Summe von 1 bis n – 1 brauchen. Das Problem lässt sich jedoch ganz leicht lösen, indem wir in der Formel jedes n durch n – 1 ersetzen.

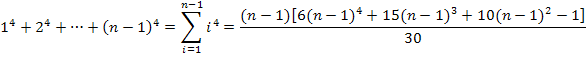
Den entstandenen Term vereinfachen wir in einer Nebenrechnung. Um die Klammern bei 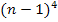und 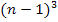aufzulösen, verwenden wir hier das Pascalsche Dreieck. Du kannst aber stattdessen auch 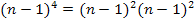und bei 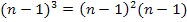rechnen. Das ist bloßsehr viel Arbeit. 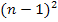kannst du mit der zweiten binomischen Formelausrechnen.

Nebenrechnung:

Mit 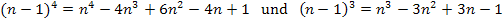ergibt sich:

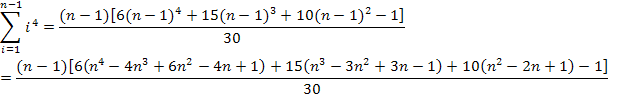
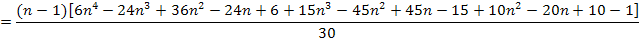
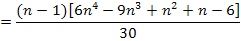
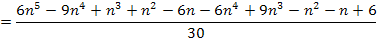
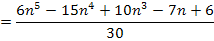
Damit ergibt sich für die Untersumme mit n Streifen:

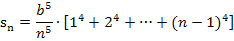
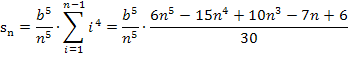
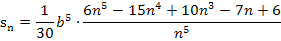
Letztendlich wollen wir die Streifenanzahl n gegen Unendlich gehen lassen. In anderen Worten:Wir müssen den Grenzwert 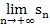berechnen.

Dazu formen wir den Bruch 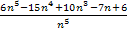noch etwas um. Wir teilen jeden Summanden des Zählers einzeln durch den Nenner .

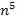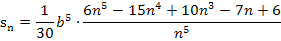
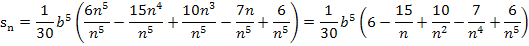
Jetzt kann der Grenzwert 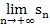leicht berechnet werden. Für n gegen Unendlich gehen die Brüche 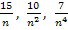und 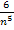nämlich gegen Null, d.h. sie werden für sehr große Werte von n vernachlässigbar klein.

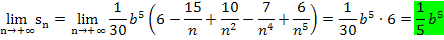
Die Ergebnisse der beiden Grenzwerte von Untersumme und Obersumme 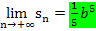und 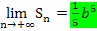sind gleich. Das Ergebnis der beiden Grenzwerte liefert den exakten Wert für das Integral.

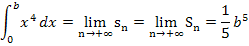
Wir haben somit die Formel für 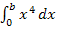hergeleitet.

Die soeben gezeigte Formel gilt nur für die untere Grenze a = 0. Nun machen wir daraus eine Formel für das Integral 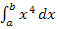, das die allgemeine untere Grenze a hat.

---