Das Summenzeichen und die Streifenmethode
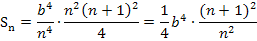
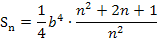
Letztendlich wollen wir die Streifenanzahl n gegen Unendlich gehen lassen. In anderen Worten:Wir müssen den Grenzwert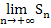 
berechnen.
Damit wir diesen Grenzwert bequem ermitteln können, formen wir den Bruch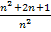 
noch etwas um. Wir teilen jeden Summanden des Zählers einzeln durch den Nenner 
.
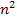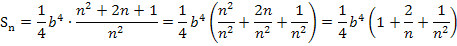
In der nun vorliegenden Form von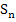 
kann der Grenzwert 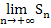leicht berechnet werden. Für n gegen Unendlich gehen die Brüche 
und 
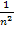nämlich gegen Null, d.h. sie werden für sehr große Werte von n vernachlässigbar klein.
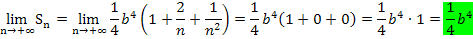
Berechnung der Untersumme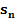 
:
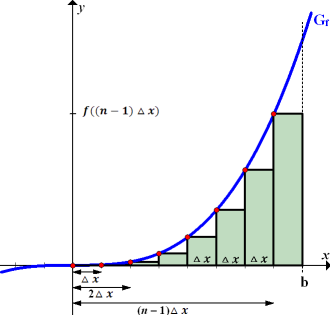
Abb. 13:Zur Berechnung der Untersumme 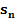im Intervall 0 bis b mit 
Hinweis:In Abb. 13 sind offensichtlich 8 Streifen dargestellt. Du musst dir allerdings vorstellen, dass es sich allgemein um n Streifen handeln soll. Zu sehen ist in Abb. 13 natürlich die Untersumme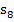 
. Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete Zahl für n zu wählen. n = 8 ist also nur ein beliebiges Beispiel. Fasse den größten und letzten Streifen am besten als den n.ten Streifen auf und nicht einfach als den achten! Entsprechend ist der vorletzte Streifen nicht als der siebte, sondern als der (n – 1).te Streifen zu verstehen.
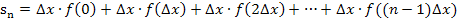
Wir klammern jetzt die Streifenbreite 
aus.
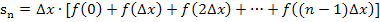
Mit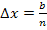 
ergibt sich:
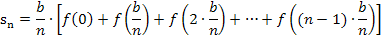
Damit du nachher leichter auf eine Gesetzmäßigkeit kommst, mit der du ein Summenzeichen einführen kannst, schreiben wir statt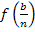 
ab sofort: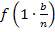 
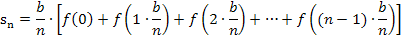
Nun setzen wir die x-Koordinaten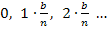 
bis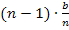 
in die gegebene Funktionsgleichung 
ein, um 
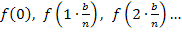bis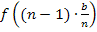 
zu ermitteln.
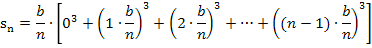
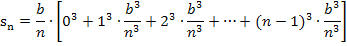
Jetzt müssen wir das Ganze noch soweit möglich vereinfachen. Wir klammern dazu wieder den Faktor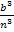 
aus. Das ergibt:
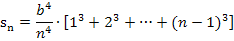
Den Ausdruck in der eckigen Klammer können wir mit dem Summenzeichen schreiben. In der Klammer steht die Summe der dritten Potenzen aller natürlichen Zahlen von 1 bis n – 1. Jetzt verwenden wir wieder die Formel für die Summe der dritten Potenzen.
Noch einmal zur Erinnerung:
Leider stehen wir nun vor dem Problem, dass diese Formel eigentlich für die Summe der dritten Potenzen von 1 bis n gilt, wir hier allerdings die Summe von 1 bis n – 1 brauchen. Das Problem lässt sich jedoch ganz leicht lösen, indem wir in der Formel jedes n durch n – 1 ersetzen.
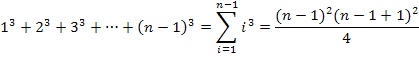
Damit ergibt sich für die Untersumme mit n Streifen:
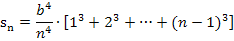
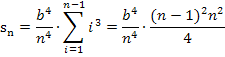
Als nächstes vereinfachen wir den entstandenen Term, indem wir mit 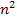kürzen und die verbleibende Klammer mit der zweiten binomischen Formelquadrieren.
