Das Summenzeichen und die Streifenmethode
Berechnung der Dreiecksfläche:
Die Katheten [AB] und [AC] besitzen hier offensichtlich die Länge 2.
Nicht klar? Ok, dann ganz ausführlich:
Die Länge von [AB] ergibt sich aus dem Unterschied der x-Koordinaten der Punkte A(-1|0) und B(1|0). Vergleiche Abbildung mit △ABC oben!
Daher gilt: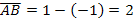 
Die Länge von [AC] ergibt sich direkt aus der y-Koordinate von C(-1|2). Vergleiche dazu noch einmal Abbildung mit △ABC oben!
Die y-Koordinate von C kann durch Einsetzen der x-Koordinate x = -1 in die Funktionsgleichung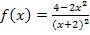 
berechnet werden, da C ein Punkt des Graphen 
ist. Somit gilt: 
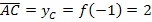
Die Fläche von △ABC wird daher folgendermaßen berechnet:
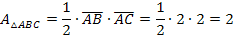
Die eigentlich gesuchte Fläche A, also das Ergebnis von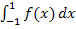 
, kann nicht kleiner sein als 
. Anders formuliert: ist eine untere Schranke für 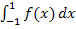. Das Integral 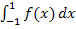ist sogar größer als .
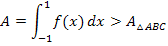
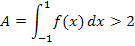
Zu 5c.)
Die gesuchte Fläche A soll durch ein geeignetes Trapez abgeschätzt werden.
Zur Erinnerung:
Ein Trapez ist ein Viereck mit zwei parallelen Seiten, Grundlinien 
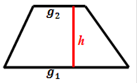
und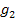 
genannt. Der Abstand der parallelen Seiten wird als Höhe h bezeichnet.
Bsp.:
Der Flächeninhalt eines Trapezes wird berechnet mit der Formel: 
Man muss also zumindest die Länge beider Grundlinien und 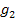sowie der Höhe h kennen, um den Flächeninhalt des Trapezes berechnen zu können. Die Grundlinien und 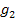sind, wie gesagt, diejenigen Seiten eines Trapezes, die zueinander parallel liegen.
Überlege dir nun, wie die gesuchte Fläche durch ein Trapez abgeschätzt werden kann! Wo liegen die Eckpunkte eines geeigneten Trapezes? Welche Seiten bilden die Grundlinien? Betrachte dazu noch einmal die Abbildung, welche die exakte Fläche A zeigt.
Hier noch einmal die Zeichnung von oben:
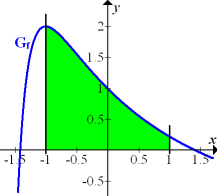
Abb.:Graph der Funktion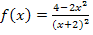 
mit der exakten Fläche A, die im Intervall [-1;1] zwischen und der x-Achse liegt (grün markiert)
Du bist hoffentlich selbst darauf gekommen, dass sich als Abschätzung der Fläche A das Trapez mit den Eckpunkten A(-1|0), B(1|0), C(1|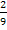 
) und D(-1|2) anbietet. Die y-Koordinate des Punkte C ergibt sich dabei aus 
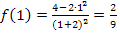, da C schließlich die x-Koordinate x = 1 hat und auf dem Graph liegt. Vergleiche folgende Abbildung!
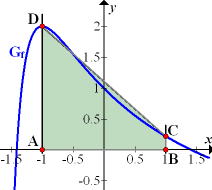
Abb.:Graph der Funktion 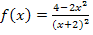mit Trapez ABCD zur Abschätzung von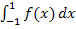
Die Seiten [AD] und [BC] verlaufen parallel zueinander, daher sind sie die Grundlinien des Trapezes ABCD. Die Seite [AB] bildet die Höhe des Trapezes. Es gilt:
Damit ergibt sich für den Flächeninhalt des Trapezes:
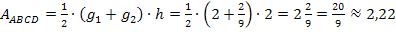
Der Flächeninhalt des Trapezes ist etwas größer als die tatsächlich gesuchte Fläche A.
