Das Summenzeichen und die Streifenmethode
Das i durchläuft demnach alle natürlichen Zahlen von der unteren Grenze bis zur oberen Grenze;in unserem letzten Beispiel die Zahlen von 1 bis 100 (jeweils einschließlich).
Hinweis:Auf dieser website wird das Summenzeichen im Fließtext kleiner geschrieben und die Grenzen direkt dahinter. Üblich ist normalerweise eher die Schreibweise mit den Grenzen unter- bzw. oberhalb des Summenzeichens. Leider lässt sich diese Schreibweise aus technischen Gründen im Fließtext nicht machen.
Nun stellt sich allerdings die Frage, wie man das Ergebnis von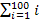 
möglichst schnell findet. Natürlich kann man der Reihe nach alle natürlichen Zahlen von 1 bis 100 addieren. Es geht aber auch wesentlich einfacher. Dazu gleich noch mehr. Vorweg schon mal das Ergebnis:
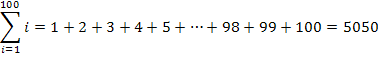
Mal sehen, ob du bisher alles verstanden hast. Was bedeutet beispielsweise die folgende Summenschreibweise:
Das bedeutet, dass der Reihe nach für i alle natürlichen Zahlen von 1 bis 6 in den Term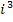 
eingesetzt und addiert werden sollen.
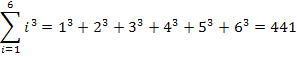
Jetzt wollen wir die Summenschreibweise noch ein bisschen üben, bevor wir zum nächsten wichtigen Punkt kommen, nämlich wie man das Ergebnis einer derartigen Summe viel schneller ausrechnen kann als durch normales Addieren der einzelnen Zahlen.
Versuche die folgenden zwei Beispielaufgaben selbständig zu lösen, bevor du dir die Lösung anschaust!
1. Bsp.:
Berechne die Ergebnisse der folgenden Summen durch normales Addieren der einzelnen Summanden!
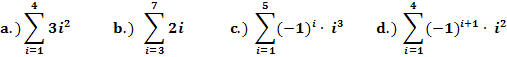
Lösung:
Zu 1a.)
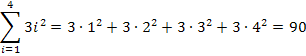
Zu 1b.)
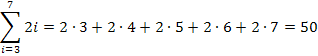
Zu 1c.)
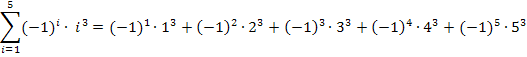
Wie du weißt, ergibt -1 hoch eine ungerade Zahl wieder -1. Bei ungeraden Exponenten bleibt bekanntlich das Minus erhalten. Ist der Exponent dagegen gerade, fällt das Minuszeichen weg. Deshalb ist -1 hoch eine gerade Zahl +1. Dadurch ergibt sich durch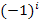 
für alle ungeraden Werte von i ein Minuszeichen und bei allen geraden Werten von i ein Pluszeichen. Die Vorzeichen wechseln somit immer zwischen Minus und Plus.
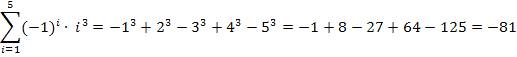
Der Ausdruck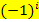 
bewirkt offensichtlich, dass die Vorzeichen immer abwechseln, für ungerade i ergibt sich Minus, für gerade i Plus.
Zu 1d.)
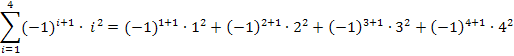
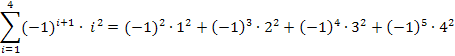
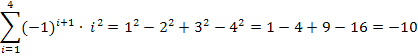
Offensichtlich bewirkt auch der Ausdruck 
einen Vorzeichenwechsel von Glied zu Glied. Doch ergibt sich bei für ungerade i Plus und für gerade i Minus, also genau umgekehrt wie bei .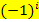
Nun versuchen wir das Ganze mal rückwärts. Gegeben ist die Summe und du sollst die Schreibweise mit dem Summenzeichen finden. Los geht´s!
