Das Summenzeichen und die Streifenmethode
Das gesamte Intervall hat eine Breite von 2. Wenn man es in 4 gleichlange Stücke zerteilt, hat jedes Stück die Länge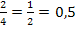 
. Die Streifenbreite ist deshalb jeweils 
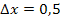. Das sieht man auch direkt an der Zeichnung.
Für die Berechnung der Streifenhöhen benötigen wir bei der Obersumme jeweils die y-Koordinate des höchsten Punktes in jedem Streifen. An der Zeichnung ist zu erkennen, dass der Graph 
im Intervall [-1;1] fallend ist. Daher liegen die für die Obersumme wichtigen Kurvenpunkte jeweils am linken Rand der Streifen, genauer gesagt in der linken oberen Ecke. (in der Abb. rot markierte Kurvenpunkte). Diese Punkte haben die folgenden x-Koordinaten:
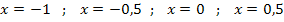
Die zugehörigen y-Koordinaten liefern die Streifenhöhen. Um sie zu berechnen, müssen wir die genannten x-Koordinaten nacheinander in die Funktionsgleichung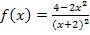 
einsetzen. (Du darfst die Streifenhöhen nicht einfach aus der Zeichnung entnehmen, das wäre viel zu ungenau.) Die Streifenhöhen ergeben sich daher aus:
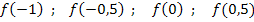
Für die Obersumme mit 4 Streifen ergibt sich demnach:
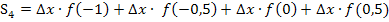
Mit :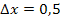
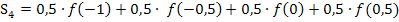
Wir setzen die jeweiligen x-Koordinaten in die Funktionsgleichung 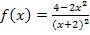ein. Das ergibt:
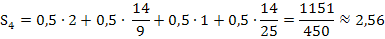
Weiter mit der Untersumme. Auch dazu fertigen wir vorweg eine Zeichnung an.
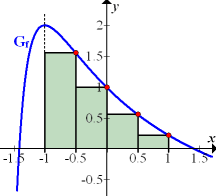
Abb.:Graph der Funktion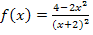 
mit Untersumme 
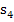zur Abschätzung von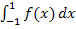 
Die Streifenbreite ist wieder jeweils 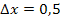. Das sieht man direkt an der Zeichnung und außerdem haben wir das bei der Obersumme schon berechnet.
Für die Berechnung der Streifenhöhen benötigen wir bei der Untersumme jeweils die y-Koordinate des tiefsten Punktes in jedem Streifen. An der Zeichnung ist zu erkennen, dass der Graph im Intervall [-1;1] fallend ist. Daher liegen die für die Untersumme wichtigen Kurvenpunkte jeweils am rechten Rand der Streifen, genauer gesagt in der rechten oberen Ecke. (in der Abb. rot markierte Kurvenpunkte). Diese Punkte haben die folgenden x-Koordinaten:
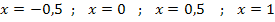
Die zugehörigen y-Koordinaten liefern die Streifenhöhen. Um sie zu berechnen, müssen wir die genannten x-Koordinaten nacheinander in die Funktionsgleichung 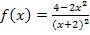einsetzen. Die Streifenhöhen ergeben sich daher aus:
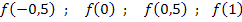
Für die Untersumme mit 4 Streifen erhalten wir demnach:
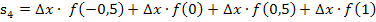
Mit :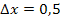
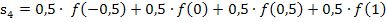
Wir setzen die jeweiligen x-Koordinaten in die Funktionsgleichung 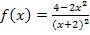ein. Das ergibt:
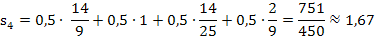
Die gesuchte Fläche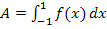 
liegt demnach zwischen der Untersumme 
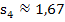und der Obersumme 
.
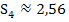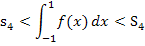
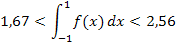
Wir berechnen noch den Mittelwert aus Ober- und Untersumme.
