Das Summenzeichen und die Streifenmethode

b.) Mit Hilfe der Fläche eines geeigneten Dreiecks

c.) Mit Hilfe der Fläche eines geeigneten Trapezes

Runde dabei auf 2 Dezimalen! Gib bei b.) und c.) auch jeweils die Koordinaten der Eckpunkte des Dreiecks bzw. Trapezes an! Handelt es sich bei der Abschätzung des Flächeninhalts A durch die Dreiecksfläche bzw. durch die Trapezfläche jeweils um eine Abschätzung nach oben oder nach unten?

Lösung:

Zuerst überlegen wir uns, wie der Graph der Funktion 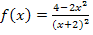insgesamt aussieht.

Du kannst dir selbst absolut nicht vorstellen, wie der Graph dieser Funktion aussehen könnte? Dann gehe zu:Allgemeine Hinweise zu der vorliegenden Funktion

Mit Hilfe einer Wertetabelle lässt sich der Graph leicht zeichnen. In der nachfolgenden Abbildung ist der Graph von 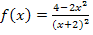mit seiner senkrechten Asymptote x = -2 und der waagrechten Asymptote y = -2 zu sehen.

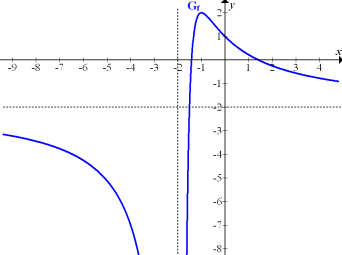
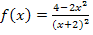Abb.:Graph der gebrochenrationalen Funktion mit seiner senkrechten Asymptote x = -2 und der waagrechten Asymptote y = -2

Die gesuchte Fläche A liegt im Intervall [-1;1]. Daher brauchen wir nur den Teil des Graphen, der in diesem Bereich liegt. Wir zeichnen den Graph nun stark vergrößert in einem Teilbereich, der das Intervall [-1;1] deutlich zeigt. Wenn du die Aufgabe alleine lösen willst, solltest du selbst eine Zeichnung auf Papier anfertigen. Wähle dazu auf beiden Achsen den Maßstab 1 LE = 2 cm! Dadurch wird die Zeichnung schön groß, so dass du die in Teilaufgabe a.) benötigten vier Streifen gut einzeichnen kannst. Zeichne den Graph beispielsweise im Intervall [-1,5;1.5] und markierte die gesuchte Fläche A!

Deine Zeichnung sollte im Prinzip aussehen wie die folgende Abbildung.

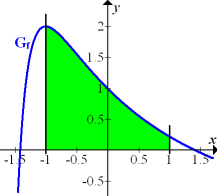
Abb.:Graph der Funktion 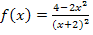mit der gesuchten Fläche A, welche im Intervall [-1;1] zwischen und der x-Achse liegt (grün markiert)

Nun geht es an die Abschätzung der Fläche A. (Exakt kannst du den Inhalt der Fläche A im Moment nicht ausrechnen, denn wir haben noch nicht besprochen, wie man 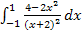exakt berechnet. Das musst du also momentan noch nicht können. Deshalb ist nur die Abschätzung der Fläche verlangt.)

Zu 5a.)

Der Inhalt der Fläche A soll mittels der Streifenmethode näherungsweise berechnet werden. Gesucht ist die Ober- und Untersumme mit 4 Streifen.

Wir beginnen mit der Obersumme. Dazu fertigen wir vorweg eine Zeichnung an.

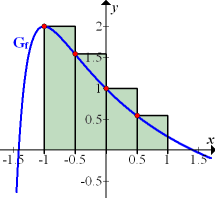
Abb.:Graph der Funktion 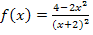mit Obersumme 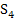zur Abschätzung von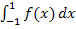

Die gesuchte Fläche liegt im Intervall [-1;1]. Es liegen 4 Streifen gleicher Breite vor.

---