Das Summenzeichen und die Streifenmethode
Nun wissen wir, wie man Integrale der Form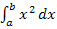 
exakt berechnet. Die Formel 
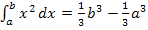gilt jedoch ausschließlich für die Integrandenfunktion 
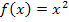. Was ist aber, wenn die Integrandenfunktion 
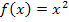nicht gerade die quadratische Funktion ist? Dann haben wir die bei 
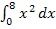oben schon vorgestellten Optionen:Entweder wir berechnen das Integral 
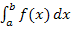näherungsweise durch Ober- bzw. Untersummenbildung mit einer konkreten Streifenanzahl n oder wir berechnen es exakt. Für die exakte Berechnung ermitteln wir zuerst allgemein die Ober- und Untersumme mit n Streifen, d.h. ohne eine konkrete Zahl für n zu wählen, und bilden dann die Grenzwerte der Ober- und Untersumme für n gegen Unendlich.
Wenn die Funktion eine kompliziertere Funktionsgleichung hat, ist es leider sehr schwierig mit der allgemeinen Streifenanzahl n zu rechnen. Deshalb ist die exakte Berechnung eines Integrals mit der Streifenmethode nur für bestimmte Grundintegrale sinnvoll. (Die Herleitungen der Grundintegrale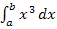 
und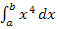 
kannst du dir auf dieser website weiter unten noch anschauen. Die gesamte Rechnung wird jeweils, wie schon bei 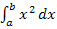, Schritt für Schritt vorgeführt.) Die Streifenmethode mit n Streifen musst du alleine nicht können, doch das Prinzip sollte dir wenigstens klar sein.
Wesentlich leichter ist die Rechnung, wenn eine konkrete Streifenanzahl vorgegeben ist. Selbst musst du nur Aufgaben zur Streifenmethode lösen können, bei denen die Streifenanzahl konkret angegeben ist. (Aufgaben mit mehr als 4 Streifen kommen in Prüfungen in der Regel nicht vor.) Du muss die Streifenmethode also mit höchstens 4 Streifen können. Vergleiche dazu auch das unten folgende Bsp. 5a.! Ähnliche Aufgaben solltest du auf jeden Fall selbständig lösen können.
Andere Möglichkeiten ein Integral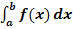 
näherungsweise zu berechnen:
Manche bestimmte Integrale lassen sich nicht nur durch Unterteilung in rechteckige Streifen näherungsweise relativ genau berechnen, sondern auch durch Berechnung des Flächeninhalts anderer geometrischer Figuren, wie zum Beispiel Dreieck oder Trapez. Die Streifenmethode liefert nicht immer die besten Abschätzungen;das hängt vom jeweiligen Einzelfall ab. So gibt es Integrale, deren Wert sich durch die Fläche eines einzigen Dreiecks oder Trapezes schon ganz gut abschätzen lässt. Schauen wir uns dazu eine konkrete Beispielaufgabe an!
5. Bsp.:
Gegeben ist die Funktion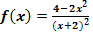 
mit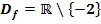 
. Berechne näherungsweise die Fläche A, welche im Intervall [-1;1] zwischen dem Graph 
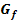und der x-Achse liegt!
a.) Mit Hilfe der Streifenmethode durch Mittelwertbildung von Ober- und Untersumme bei Verwendung von 4 Streifen gleicher Breite
