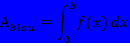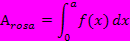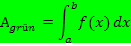Das Summenzeichen und die Streifenmethode
Nun wieder zurück zum Integral 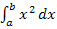 . Ursprünglich wollten wir eigentlich eine Formel für
. Ursprünglich wollten wir eigentlich eine Formel für 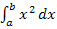 mit der allgemeinen unteren Grenze a herleiten und nicht nur eine Formel für
mit der allgemeinen unteren Grenze a herleiten und nicht nur eine Formel für 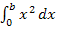 mit der besonderen unteren Grenze a = 0. Eine Formel für
mit der besonderen unteren Grenze a = 0. Eine Formel für 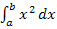 lässt sich entweder direkt mit der Streifenmethode herleiten, was aber einen ziemlich großen Rechenaufwand bedeutet, oder einfacher aus der Formel
lässt sich entweder direkt mit der Streifenmethode herleiten, was aber einen ziemlich großen Rechenaufwand bedeutet, oder einfacher aus der Formel 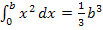 folgern. Wir wollen hier den einfacheren Weg wählen und von der bereits hergeleiteten Formel
folgern. Wir wollen hier den einfacheren Weg wählen und von der bereits hergeleiteten Formel 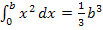 ausgehen.
ausgehen.
Wenn die Formel 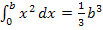 gilt, muss entsprechend auch
gilt, muss entsprechend auch 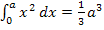 gelten. (Die Bezeichnung b für die obere Grenze wurde dabei rein formal durch den Buchstaben a ersetzt.) Wir wissen also, wie man
gelten. (Die Bezeichnung b für die obere Grenze wurde dabei rein formal durch den Buchstaben a ersetzt.) Wir wissen also, wie man 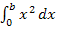 und
und 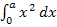 berechnet. Wir suchen aber
berechnet. Wir suchen aber 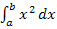 .
.
Aus den Integralen 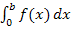 und
und 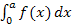 lässt sich generell für beliebige Integrandenfunktionen
lässt sich generell für beliebige Integrandenfunktionen  das Integral
das Integral 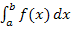 ableiten. Betrachte dazu die nachfolgenden Abbildungen!
ableiten. Betrachte dazu die nachfolgenden Abbildungen!
|
|
|
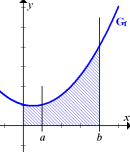
Das Integral 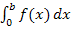 entspricht der blau schraffierten Fläche in der Abbildung oben links. Das Integral
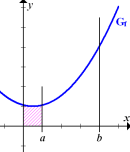
entspricht der blau schraffierten Fläche in der Abbildung oben links. Das Integral 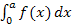 entspricht der rosa schraffierten Fläche in der Abbildung oben Mitte. Das eigentlich gesuchte Integral
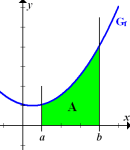
entspricht der rosa schraffierten Fläche in der Abbildung oben Mitte. Das eigentlich gesuchte Integral 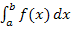 entspricht der grünen Fläche A in der Abbildung oben rechts.
entspricht der grünen Fläche A in der Abbildung oben rechts.
Das Integral 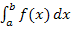 (grüne Fläche) ergibt sich, wenn man vom Integral
(grüne Fläche) ergibt sich, wenn man vom Integral 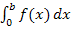 (blau schraffierte Fläche) das Integral
(blau schraffierte Fläche) das Integral 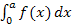 (rosa schraffierte Fläche) abzieht. Daher gilt allgemein:
(rosa schraffierte Fläche) abzieht. Daher gilt allgemein:
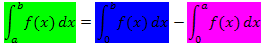
Auf unsere Funktion 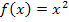 angewendet, bedeutet das:
angewendet, bedeutet das:
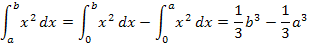
Damit haben wir auch eine Formel für 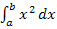 hergeleitet:
hergeleitet:
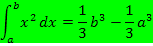
In der nachfolgenden Abbildung (Abb. 10) kannst du die Fläche sehen, deren Inhalt du mit dieser Formel berechnen kannst. Vergleiche dazu die grün markierte Fläche A in Abb. 10!
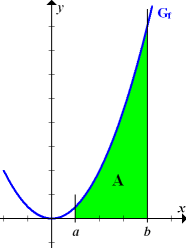
Abb. 10:Graph 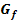 der Funktion
der Funktion 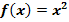 mit
mit 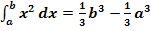 (grün markierte Fläche A)
(grün markierte Fläche A)
Du möchtest noch wissen, wie man das Integral 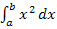 mit der allgemeinen unteren Grenze a
mit der allgemeinen unteren Grenze a 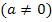 direkt mit der Streifenmethode berechnen kann? Dann gehe zu:Streifenmethode für Integrale mit der allgemeinen unteren Grenze a
direkt mit der Streifenmethode berechnen kann? Dann gehe zu:Streifenmethode für Integrale mit der allgemeinen unteren Grenze a
Sind a und b konkrete Zahlen, musst du sie nur in die Formel 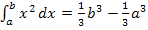 einsetzen und das Ergebnis ausrechnen.
einsetzen und das Ergebnis ausrechnen.
4. Bsp.:Berechne 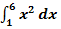 !
!
Lösung:
Es gilt:Untere Grenze a = 1 Obere Grenze b = 6
Wir setzen diese Werte in die Formel 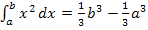 ein und berechnen das Ergebnis.
ein und berechnen das Ergebnis.
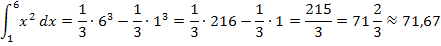
Hinweis:Später wirst du noch eine andere Methode lernen, wie du mit Hilfe der Stammfunktion F(x) bestimmteIntegrale berechnen kannst. Am Ende dieses Teils werden wir noch einmal kurz darauf zurückkommen. (Mehr dazu auch im Teil Das bestimmte und das unbestimmte Integral.)