Das Summenzeichen und die Streifenmethode
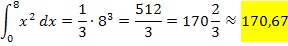
Die Fläche zwischen 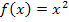 und der x-Achse von x = 0 bis x = 8 hat somit exakt den Wert
und der x-Achse von x = 0 bis x = 8 hat somit exakt den Wert 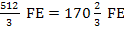 . (Dabei steht FE für Flächeneinheiten, z. B.
. (Dabei steht FE für Flächeneinheiten, z. B. 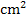 .)
.)
Vergleiche nun zum Abschluss das exakte Ergebnis mit den Näherungswerten, die wir durch die Mittelwertbildung von Ober- und Untersumme mit 2, 4 und 8 Streifen erhielten!
Hier noch einmal die Ergebnisse von oben:
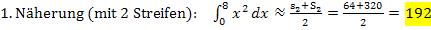
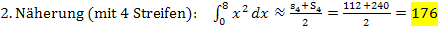
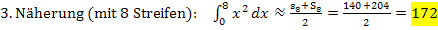
Die 2. und vor allem die 3. Näherung ergeben offensichtlich schon ganz passable Werte, wobei natürlich die Genauigkeit der Näherung mit steigender Streifenanzahl zunimmt.
Wir halten allgemein fest:
Das Integral 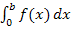 lässt sich mit Hilfe der Streifenmethode berechnen. Die Ergebnisse der Ober- und Untersumme nähern sich mit größer werdender Streifenanzahl n immer mehr an den exakten Wert des Integrals an. Die Grenzwerte von Ober- und Untersumme für n gegen Unendlich liefern den exakten Wert.
lässt sich mit Hilfe der Streifenmethode berechnen. Die Ergebnisse der Ober- und Untersumme nähern sich mit größer werdender Streifenanzahl n immer mehr an den exakten Wert des Integrals an. Die Grenzwerte von Ober- und Untersumme für n gegen Unendlich liefern den exakten Wert.
Wie die Ober- und Untersumme berechnet wird, hängt davon ab, ob die Integrandenfunktion  im jeweiligen Intervall steigt oder fällt.
im jeweiligen Intervall steigt oder fällt.
Übersicht zur Berechnung des Integrals 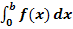 mit der Streifenmethode:
mit der Streifenmethode:
Ist die untere Grenze a = 0 gilt allgemein für die Streifenbreite: 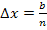
Bei Funktionen  , die im Intervall von 0 bis b streng monoton steigend sind, gelten folgende allgemeine Ansätze für Ober- bzw. Untersumme.
, die im Intervall von 0 bis b streng monoton steigend sind, gelten folgende allgemeine Ansätze für Ober- bzw. Untersumme.
Obersumme: 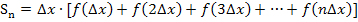
Untersumme:
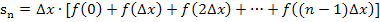
Bei Funktionen  , die im Intervall von 0 bis b streng monoton fallend sind, gelten dagegen folgende allgemeine Ansätze für Ober- bzw. Untersumme.
, die im Intervall von 0 bis b streng monoton fallend sind, gelten dagegen folgende allgemeine Ansätze für Ober- bzw. Untersumme.
Obersumme: 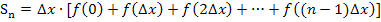
Untersumme:
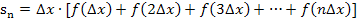
Es fällt auf:Bei streng monoton fallenden Funktionen  sind die Ansätze von Ober- und Untersumme genau vertauscht im Vergleich zu streng monoton steigenden Funktionen. Warum ist das so?
sind die Ansätze von Ober- und Untersumme genau vertauscht im Vergleich zu streng monoton steigenden Funktionen. Warum ist das so?
Bei streng monoton steigenden Funktionen liegen die für die Berechnung der Streifenhöhen benötigten Kurvenpunkte bei der Obersumme immer am rechten Rand der einzelnen Streifen und bei der Untersumme am linken Rand. (Betrachte dazu die nachfolgenden Abbildungen I und II.)
Bei streng monoton fallenden Funktionen ist es genau umgekehrt. Ist die Integrandenfunktion  streng monoton fallend, liegen die Kurvenpunkte, deren y-Koordinaten die Streifenhöhen liefern, bei der Obersumme immer am linken Rand und bei der Untersumme immer am rechten Rand der Streifen. (Betrachte dazu die nachfolgenden Abbildungen III und IV.)
streng monoton fallend, liegen die Kurvenpunkte, deren y-Koordinaten die Streifenhöhen liefern, bei der Obersumme immer am linken Rand und bei der Untersumme immer am rechten Rand der Streifen. (Betrachte dazu die nachfolgenden Abbildungen III und IV.)
Deshalb sind die Ansätze für Ober- und Untersumme bei fallenden Funktionen genau umgekehrt wie bei steigenden Funktionen.
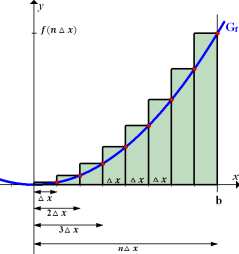
Abb. I:Obersumme Die Kurvenpunkte, die zur Berechnung der Streifenhöhen benötigt werden, liegen jeweils am rechten Rand der Streifen. |
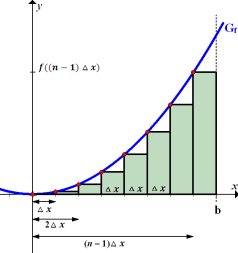
Abb. II:Untersumme Die Kurvenpunkte, die zur Berechnung der Streifenhöhen benötigt werden, liegen jeweils am linken Rand der Streifen. |
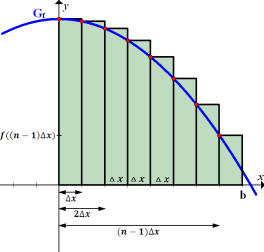
Abb. III:Obersumme Die Kurvenpunkte, die zur Berechnung der Streifenhöhen benötigt werden, liegen jeweils am linken Rand der Streifen. |
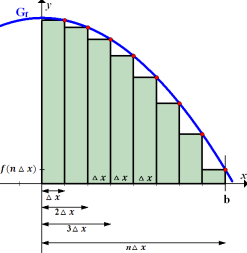
Abb. IV:Untersumme Die Kurvenpunkte, die zur Berechnung der Streifenhöhen benötigt werden, liegen jeweils am rechten Rand der Streifen. |

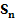 einer im Intervall [a; b] steigenden Funktion
einer im Intervall [a; b] steigenden Funktion 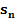 einer im Intervall [a; b] steigenden Funktion
einer im Intervall [a; b] steigenden Funktion 