Das Summenzeichen und die Streifenmethode
Leider stehen wir nun vor dem Problem, dass diese Formel eigentlich für die Summe der Quadratzahlen von 1 bis n gilt, wir hier allerdings die Summe von 1 bis n – 1 brauchen. Das Problem lässt sich jedoch ganz leicht lösen, indem wir in der Formel jedes n durch n – 1 ersetzen. (Wollte man beispielsweise die Summe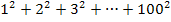 
mit Hilfe der Formel berechnen, müsste man jedes n durch die Zahl 100 ersetzen. Entsprechend wird hier für n nun n – 1 eingesetzt.)
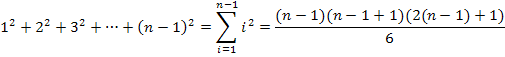
Damit ergibt sich für die Untersumme mit n Streifen:
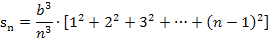
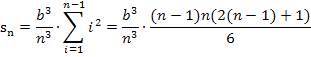
Als nächstes vereinfachen wir den entstandenen Term, indem wir in der hinteren Klammer die Zahl 2 in die Klammer (n – 1) hineinmultiplizieren, mit n kürzen und die verbleibenden Klammern ausmultiplizieren. Statt durch 6 zu teilen, multiplizieren wir mit dem Kehrwert von 6, also mit 
. Dann sieht das Ganze schöner aus. Nach dem Kürzen mit n verbleibt noch 
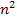im Nenner des ersten Bruchs. Dieses 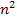schreiben wir besser in den Nenner des zweiten Bruchs. Dann lässt sich nachher leichter weiterrechnen. Die Rechnung funktioniert so ähnlich wie die Vereinfachung der Obersumme 
.
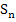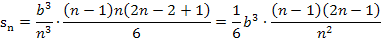
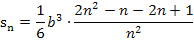
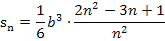
Letztendlich wollen wir die Streifenanzahl n gegen Unendlich gehen lassen. In anderen Worten:Wir müssen den Grenzwert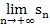 
berechnen.
Damit wir diesen Grenzwert bequem ermitteln können, formen wir den Bruch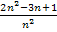 
noch etwas um. Wir teilen jeden Summanden des Zählers einzeln durch den Nenner .
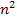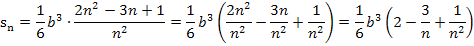
In der nun vorliegenden Form von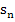 
kann der Grenzwert 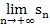leicht berechnet werden. Für n gegen Unendlich gehen die Brüche 
und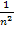 
nämlich gegen Null, d.h. sie werden für sehr große Werte von n vernachlässigbar klein.
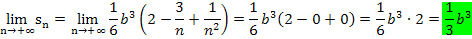
Wenn wir die Ergebnisse der beiden Grenzwerte von Untersumme und Obersumme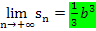 
und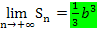 
miteinander vergleichen, stellen wir fest, dass die Ergebnisse gleich sind. Nur wenn 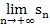und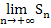 
das gleiche Ergebnis liefern, ist das Integral 
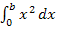überhaupt definiert. Es muss also immer das Gleiche bei 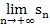und 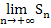herauskommen, sonst hast du dich verrechnet. Das Ergebnis der beiden Grenzwerte liefert den exakten Wert für das Integral.
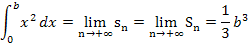
Wir haben somit eine allgemeine Formel für Integrale der Form 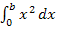hergeleitet.
Mit Hilfe dieser Formel können wir nun auch den exakten Wert des Integrals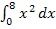 
ermitteln, dessen Wert wir zu Beginn durch Ober- und Untersummenbildung mit 2, 4 und 8 Streifen abgeschätzt haben. In der Formel 
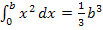steht b für die obere Grenze. Beim Integral 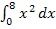ist die obere Grenze die Zahl 8. Daher gilt:b = 8
Um das Ergebnis des Integrals 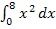exakt zu berechnen, müssen wir daher in der Formel 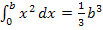nur für b die Zahl 8 einsetzen.
