Das Summenzeichen und die Streifenmethode
) Da der Graph streng monoton steigend ist, gehört zur niedrigsten y-Koordinate auch die niedrigste x-Koordinate im jeweiligen Streifen. Daher liegen die entsprechenden Punkte immer am linken Rand des Streifens. (In Abb. 9 rot markierte Punkte) Diese Punkte liegen also immer in der linken, oberen Ecke der einzelnen Streifen. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der entsprechenden x-Koordinaten in die Funktion 
.
Welche x-Koordinaten haben diese Kurvenpunkte? In Abb. 9 ist zu erkennen, dass der erste Punkt (von links) die x-Koordinate 0 hat, denn es ist der Ursprung des Koordinatensystems. Der zweite Punkt hat die x-Koordinate 
, der dritte Punkt 
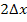usw. bis zum n .ten und letzten Punkt, der bei der Untersumme die x-Koordinate 
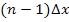besitzt.
Der erste Streifen (von links) ist hier eigentlich gar kein Rechteck, sondern nur ein waagrechter Strich, was daran liegt, dass seine Höhe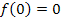 
ist. Der zweite Streifen hat die Höhe 
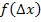, der dritte Streifen 
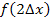usw. bis zum n.ten und letzten Streifen, der die Höhe 
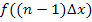besitzt. Betrachte dazu noch einmal Abb. 9!
Nun berechnen wir die Untersumme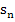 
, indem wir bei jedem der n Streifen „Breite mal Höhe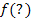 
“ rechnen und alle Ergebnisse addieren.
Beachte, dass sich zwar die x-Koordinaten ändern, die in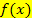 
eingesetzt werden sollen, nicht aber die Streifenbreite 
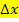. Alle Streifen haben schließlich die gleiche Breite , nur die Höhe der Streifen hängt von der x-Koordinate des entsprechenden Kurvenpunkts ab.
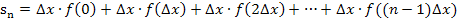
Wir klammern jetzt die Streifenbreite aus.
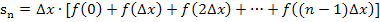
Mit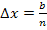 
ergibt sich:
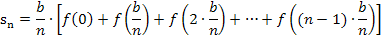
Damit du nachher leichter auf eine Gesetzmäßigkeit kommst, mit der du ein Summenzeichen einführen kannst, schreiben wir statt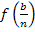 
ab sofort: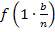 
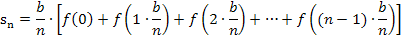
Nun setzen wir die x-Koordinaten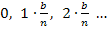 
bis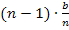 
in die gegebene Funktionsgleichung 
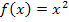ein, um 
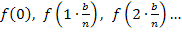bis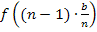 
zu ermitteln.
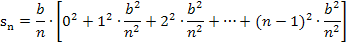
Jetzt müssen wir das Ganze noch soweit möglich vereinfachen. Was würdest du machen?
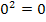Deshalb können wir „ 
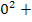“ natürlich weglassen. Die Zahlen 1 und 2 … quadrieren? Das bringt uns leider nicht weiter. Wir rechnen die Quadrate besser nicht aus. Das haben wir ja auch oben bei der Obersumme 
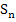so gemacht. Wir klammern besser wieder den Faktor 
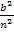aus. Das ergibt:
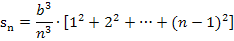
Den Ausdruck in der eckigen Klammer können wir mit dem Summenzeichen schreiben. In der Klammer steht die Summe der Quadrate aller natürlichen Zahlen von 1 bis n – 1. Jetzt verwenden wir wieder die Formel für die Summe der Quadratzahlen.
Noch einmal zur Erinnerung:
