Das Summenzeichen und die Streifenmethode
bis zum n.ten und letzten Streifen, der dann die Höhe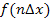 
haben muss.
Nun berechnen wir die Obersumme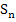 
, indem wir bei jedem der n Streifen „Breite 
mal Höhe 
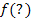“ rechnen und alle Ergebnisse addieren.
Beachte, dass sich zwar die x-Koordinaten ändern, die in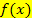 
eingesetzt werden sollen, nicht aber die Streifenbreite 
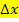. Alle Streifen haben schließlich die gleiche Breite , nur die Höhe der Streifen hängt von der x-Koordinate des entsprechenden Kurvenpunkts ab.
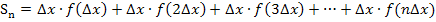
Wir klammern jetzt die Streifenbreite aus.
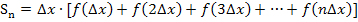
Als nächstes müssen wir durch b und n ausdrücken, da wir die Obersumme ausschließlich in Abhängigkeit von b und n berechnen wollen. Der Ausdruck soll im Ergebnis nicht mehr vorkommen;nur noch b und n dürfen letztendlich enthalten sein. Wie kann man also aus b und n berechnen? Da die Fläche (zwischen 
und der x-Achse) von 0 bis b gesucht ist, hat die gesamte Intervallbreite den Wert b. Die Strecke b wird in n gleich lange Stücke geteilt. Dann hat jedes einzelne Stück die Länge 
. Das entspricht exakt der Breite eines der Streifen.
Daher gilt für die Streifenbreite :
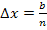
Damit ergibt sich für die Obersumme:
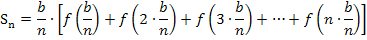
Anmerkung:Der Ausdruck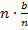 
wird absichtlich nicht gekürzt. An späterer Stelle wirst du sehen, warum wir hier mit 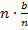weiterrechnen und nicht einfach mit b.
Damit du nachher die Gesetzmäßigkeit leichter erkennen kannst, die sich ergeben wird, schreiben wir statt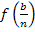 
ab sofort besser: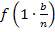 
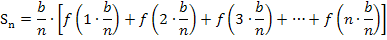
Dieser Ansatz gilt bei allen streng monoton steigenden Funktionen für die Obersumme. Ab jetzt werden wir aber konkret mit der Funktion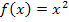 
rechnen.
Um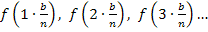 
bis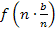 
zu ermitteln, setzen wir nun für x die Werte 
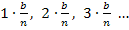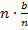bis in die gegebene Funktionsgleichung 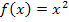ein.
Nicht klar? Dann überlege dir mal, wie du beispielsweise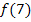 
berechnen würdest. Dafür müsstest du die Zahl 7 für x in die Funktionsgleichung 
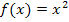einsetzen.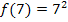 
Entsprechend werden hier 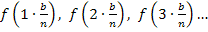bis 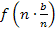gebildet. Statt der Zahl 7, die nur ein willkürlich gewähltes Beispiel war, müssen wir hier natürlich die Werte 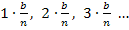bis 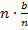in die gegebene Funktionsgleichung 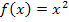für x einsetzen.
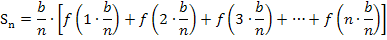
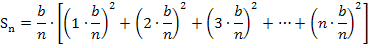
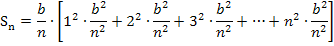
Jetzt müssen wir das Ganze soweit möglich vereinfachen. Was würdest du machen?
Die Zahlen 1, 2, 3 … quadrieren? Das bringt uns leider nicht weiter. Wir rechnen die Quadrate besser nicht aus. Warum, das siehst du etwas weiter unten. Was kann man aber sonst noch machen?
Richtig, wir klammern zusätzlich zu auch noch den Faktor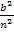 
aus. Dass sich hier 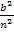ausklammern lässt, ist an der oben gezeigten Form leicht zu erkennen.
