Das Summenzeichen und die Streifenmethode
Nur so können wir die Grenzwerte der Ober- und Untersumme für n gegen Unendlich berechnen.
Ab jetzt wird es wirklich ziemlich schwierig. Bitte nicht gleich resignieren und aufgeben! Versuche Schritt für Schritt die folgende Herleitung nachzuvollziehen. Alleine musst du das nicht können. Kein vernünftiger Lehrer wird so etwas in einer Klausur verlangen. Dennoch solltest du dich wenigstens einmal mit der Herleitung der Formel für ein bestimmtes Integral beschäftigen, da in bayerischen Gymnasien die Herleitung nun mal auch im Mathe-Unterricht besprochen wird. Also, los geht´s!
Mit der Streifenmethode zu berechnen: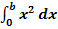 
Es gilt somit:
Untere Grenze a = 0, obere Grenze b und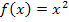 
Anzahl der Streifen:n
Berechnung der Obersumme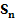 
:
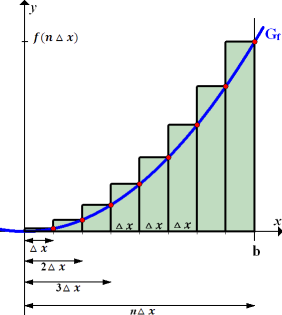
Abb. 8:Zur Berechnung der Obersumme 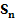im Intervall 0 bis b mit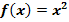 
Hinweis:In Abb. 8 sind offensichtlich 8 Streifen dargestellt, doch musst du dir vorstellen, dass es sich allgemein um n Streifen handeln soll. Zu sehen ist in Abb. 8 also natürlich die Obersumme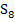 
. Leider lassen sich n Streifen nicht darstellen, ohne eine konkrete, natürliche Zahl für n zu wählen. n = 8 ist nur als beliebiges Beispiel anzusehen. Betrachte den letzten Streifen am besten als den n.ten Streifen und nicht einfach als den achten!
Alle n Streifen besitzen die gleiche Streifenbreite 
. Die Streifenhöhe ergibt sich jeweils aus der y-Koordinate des höchsten Kurvenpunktes innerhalb der einzelnen Streifen. (Bei der Obersumme wird schließlich die Oberkante des Streifens immer vom höchsten Kurvenpunkt des Streifens ausgehend gezeichnet.) Da der Graph streng monoton steigend ist, gehört zur höchsten y-Koordinate auch die höchste x-Koordinate im jeweiligen Streifen. Daher liegen die entsprechenden Punkte immer am rechten Rand des Streifens. (In Abb. 8 rot markierte Punkte) Diese Punkte liegen also immer in der rechten, oberen Ecke der einzelnen Streifen. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der entsprechenden x-Koordinaten in die Funktion 
.
Nun stellt sich allerdings die Frage, welche x-Koordinaten diese Punkte besitzen. In Abb. 8 ist zu erkennen, dass der erste Punkt (von links) die x-Koordinate besitzt. Der zweite Punkt (von links) hat die x-Koordinate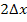 
, der dritte Punkt 
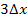usw. bis zum n.ten und letzten Punkt, der die x-Koordinate 
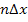besitzt. Dabei gilt: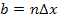 
Der erste Streifen (von links) besitzt daher die Höhe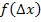 
, der zweite Streifen entsprechend 
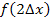, der dritte Streifen 
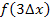usw.
