Das Summenzeichen und die Streifenmethode
Die Streifenbreite 
ergibt sich, wie schon bei der Obersumme aus der Intervallbreite b – a = 8 – 0 = 8 und der Anzahl n (hier n = 
der Streifen: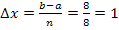 
Dass bei 8 Streifen im Intervall von 0 bis 8 für die Streifenbreite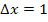 
gilt, ist klar. Das erkennt man auch an der nachfolgenden Abbildung.
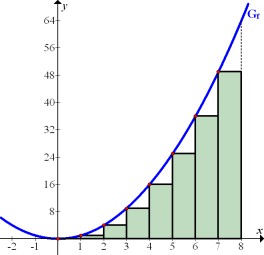
Abb. 7:Zur Berechnung der Untersumme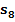 
im Intervall 0 bis 8 mit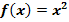 
Die Streifenhöhen ergeben sich aus den y-Koordinaten der tiefsten Kurvenpunkte innerhalb der einzelnen Streifen. (In Abb. 7 rot markierte Punkte) Diese Punkte liegen also wie immer bei Untersummen streng monoton steigender Graphen in der linken, oberen Ecke des entsprechenden Streifens. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man jeweils durch Einsetzen der x-Koordinaten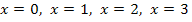 
bis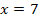 
in die Funktionsgleichung 
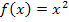. Die Streifenhöhen ergeben sich demnach aus 
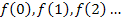bis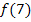 
.
Nun können wir leicht die Untersumme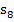 
berechnen, indem wir wieder bei jedem Streifen „Breite mal Höhe“ rechnen und alle acht Ergebnisse addieren.
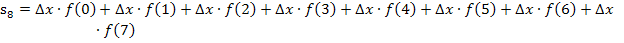
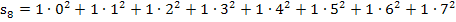
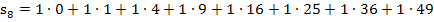
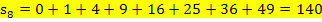
Mittelwertbildung aus Ober- und Untersumme:
Der exakte Inhalt der gesuchten Fläche A muss somit zwischen der Untersumme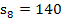 
und der Obersumme 
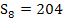liegen. Wir bilden noch das arithmetische Mittel, d.h. den Durchschnitt, von 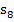und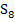 
. Das ergibt den dritten Näherungswert für 
.
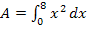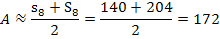
Dieser Näherungswert ist noch etwas genauer, als der, den wir vorher mit nur vier Streifen ermittelt haben.
Nun könnten wir ewig so weiter machen, d.h. die Streifenanzahl immer weiter erhöhen und immer jeweils den Mittelwert aus Unter- und Obersumme bilden. Auf das wirklich exakte Ergebnis käme man so aber niemals, denn erst mit unendlich vielen Streifen erhielte man den exakten Wert.
Im Folgenden soll eine allgemeine Formel zur exakten Berechnung des bestimmten Integrals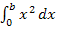 
hergeleitet werden. Als obere Grenze verwenden wir ab sofort nicht mehr den Wert 8 wie in den Beispielen bisher, sondern den Buchstaben b. Dann bekommen wir nämlich gleich eine Formel, die nicht nur für b = 8 gilt, sondern allgemein für eine beliebige obere Grenze b. Der Buchstabe b steht dabei für eine feste Zahl. Zur Vereinfachung gehen wir davon aus, dass b für eine positive Zahl steht. (Die Formel, die wir nun herleiten werden, gilt an sich sogar für beliebige reelle Zahlen b, also auch für 
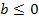. Wir verzichten hier nur auf die Herleitung für 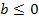, da diese Herleitung schon für b >0 schwierig genug ist.) Da wir letztendlich die Streifenanzahl n gegen Unendlich gehen lassen müssen, setzen wir auch für n keine konkrete Zahl mehr ein.
