Das Summenzeichen und die Streifenmethode

Die Höhe des kleineren Rechtecks entspricht der y-Koordinate des Kurvenpunktes mit der x-Koordinate x = 4, d.h. die Höhe des ersten Rechtecks (von links gesehen) ergibt sich hier aus 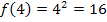. (Betrachte dazu noch einmal Abb. 2!) Der Flächeninhalt 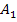des kleineren Rechtecks wird demnach berechnet durch:

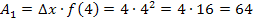
Die Höhe des größeren Rechtecks entspricht der y-Koordinate des Kurvenpunktes mit der x-Koordinate x = 8, d.h. die Höhe des zweiten Rechtecks (von links) ergibt sich hier aus 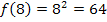. (Siehe noch einmal Abb. 2!) Der Flächeninhalt 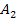des größeren Rechtecks wird demnach berechnet durch:

Die gesamte Obersumme ergibt sich aus der Summe von und :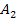

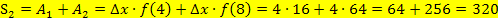
Berechnung der Untersumme :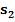

Die Streifenbreite ergibt sich, wie schon bei der Obersumme, aus der Intervallbreite b – a = 8 – 0 = 8 und der Anzahl n (hier n = 2) der Streifen: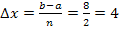

Dass bei 2 Streifen im Intervall von 0 bis 8  für die Streifenbreite 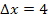gilt, erkennt man auch direkt an der nachfolgenden Abbildung.

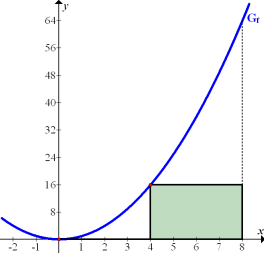
Abb. 3:Zur Berechnung der Untersumme 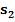im Intervall 0 bis 8 mit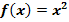

Bei der Untersumme wird in jedem Streifen von der y-Koordinate des Kurvenpunktes von 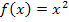ausgegangen, der am tiefsten liegt. Da der Graph von 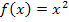für positive Werte von x streng monoton steigend ist, liegen die Kurvenpunkte mit der jeweils niedrigsten y-Koordinate immer am linken Rand der Streifen. Die Punkte sind in der Abb. 3 rot markiert.

Der erste Punkt liegt hier im Koordinatenursprung. Daher hat der erste „Streifen“ (von links gesehen) die Höhe 0;es gibt bei dieser Funktion praktisch gar kein Rechteck das zum ersten Streifen gehört. Der Flächeninhalt 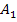des ersten Streifens ist gleich 0. Das ist aber nicht bei allen Funktionen so. Nur wegen 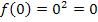ergibt sich für die Fläche des ersten „Streifens“ hier:

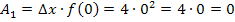
Die Höhe des zweiten Streifens ergibt sich aus der y-Koordinate des Punktes mit der x-Koordinate x = 4. D.h. die Höhe dieses Rechtecks wird berechnet durch 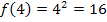. Der Flächeninhalt 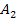des zweiten Streifens wird daher folgendermaßen berechnet:

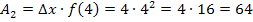
Die gesamte Untersumme 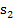ergibt sich aus der Summe von 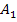und :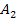

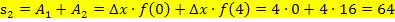
Mittelwertbildung aus Ober- und Untersumme:

Der exakte Inhalt der gesuchten Fläche A muss somit zwischen der Untersumme 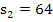und der Obersumme 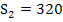liegen. Wir bilden noch das arithmetische Mittel, d.h. den Durchschnitt, von 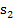und 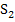. Das ergibt einen groben Näherungswert für .

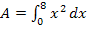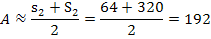
Tipp:Wenn du alleine eine Berechnung mit der Streifenmethode durchführen musst, solltest du dir immer vorweg jeweils eine Skizze zur Obersumme und eine zur Untersumme anfertigen. Dadurch kommst du wesentlich leichter auf die richtigen Ansätze für Obersumme und Untersumme! Versuche es doch gleich einmal selbst an diesem Beispiel, mit 4 Streifen und mit 8 Streifen jeweils Ober- und Untersumme zu berechnen!

---